IRIS數(shù)據(jù)集簡介
IRIS數(shù)據(jù)集中的數(shù)據(jù)源于1936年費(fèi)希爾法發(fā)表的一篇論文。彼時(shí)他收集了三種鳶尾花(分別標(biāo)記為setosa、versicolor和virginical)的花萼和花瓣數(shù)據(jù)。包括花萼的長度和寬度,以及花瓣的長度和寬度。我們將根據(jù)這四個(gè)特征來建立支持向量機(jī)模型從而實(shí)現(xiàn)對三種鳶尾花的分類判別任務(wù)。
有關(guān)數(shù)據(jù)可以從datasets軟件包中的iris數(shù)據(jù)集里獲取,下面我們演示性地列出了前5行數(shù)據(jù)。成功載入數(shù)據(jù)后,易見其中共包含了150個(gè)樣本(被標(biāo)記為setosa、versicolor和virginica的樣本各50個(gè)),以及四個(gè)樣本特征,分別是Sepal.Length、Sepal.Width、Petal.Length和Petal.Width。
> iris Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa 7 4.6 3.4 1.4 0.3 setosa 8 5.0 3.4 1.5 0.2 setosa 9 4.4 2.9 1.4 0.2 setosa 10 4.9 3.1 1.5 0.1 setosa
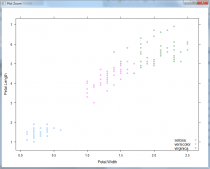
在正式建模之前,我們也可以通過一個(gè)圖型來初步判定一下數(shù)據(jù)的分布情況,為此在R中使用如下代碼來繪制(僅選擇Petal.Length和Petal.Width這兩個(gè)特征時(shí))數(shù)據(jù)的劃分情況。
library(lattice)
xyplot(Petal.Length ~ Petal.Width, data = iris,
groups = Species,
auto.key = list(corner=c(1, 0)))
上述代碼的執(zhí)行結(jié)果如圖14-13所示,從中不難發(fā)現(xiàn),標(biāo)記為setosa的鳶尾花可以很容易地被劃分出來。但僅使用Petal.Length和Petal.Width這兩個(gè)特征時(shí),versicolor和virginica之間尚不是線性可分的。
函數(shù)svm()在建立支持向量機(jī)分類模型時(shí)有兩種方式。第一種是根據(jù)既定公式建立模型,此時(shí)的函數(shù)使用格式為:
svm(formula, data= NULL, subset, na.action = na.omit , scale= TRUE)
其中:
- formula表示函數(shù)模型的形式
- data表示在模型中包含的有變量的一組可選格式數(shù)據(jù)
- 參數(shù)na.action用于指定當(dāng)樣本數(shù)據(jù)中存在無效的空數(shù)據(jù)時(shí)系統(tǒng)應(yīng)該進(jìn)行怎樣的處理。默認(rèn)值na.omit表示程序會忽略那些數(shù)據(jù)缺失的樣本。另外一個(gè)可選的賦值為na.fail,它指示系統(tǒng)在遇到空數(shù)據(jù)時(shí)給出一條錯(cuò)誤信息。
- 參數(shù)scale為一個(gè)邏輯向量指定特征是護(hù)具是否需要標(biāo)準(zhǔn)化(默認(rèn)標(biāo)準(zhǔn)化為均值0,方差1)
- 索引向量subset用于指定那些將來將被用來訓(xùn)練模型的采樣數(shù)據(jù)。
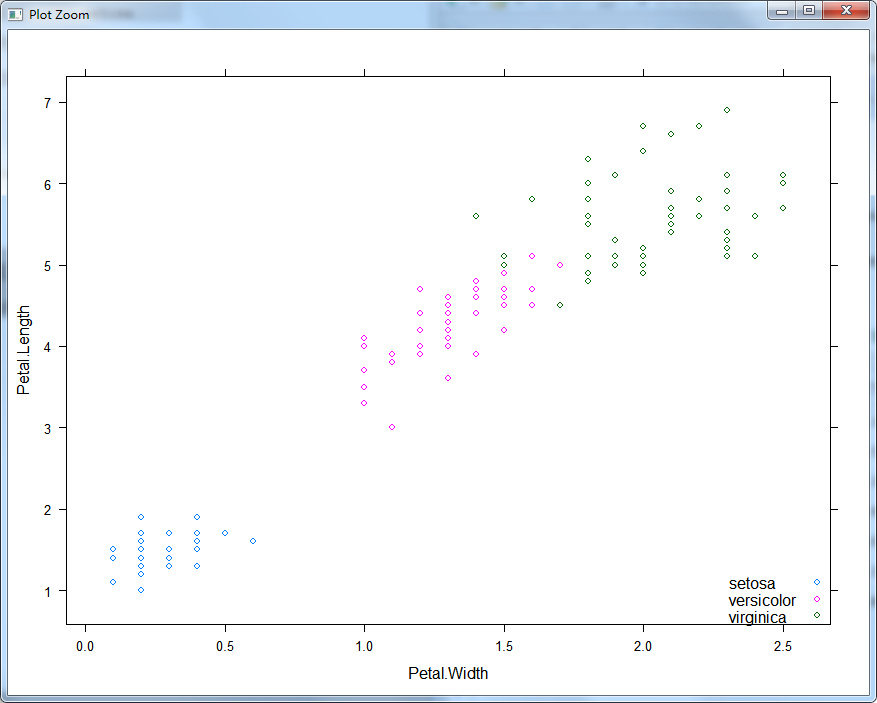
例如,已經(jīng)知道僅用Petal.Length和Petal.Width這兩個(gè)特征時(shí)標(biāo)記為setosa和versicolor的鳶尾花是線性可分的,所以我們用下面的代碼來構(gòu)建SVM模型:
data(iris)
attach(iris)
subdata <- iris[iris$Species != 'virginica', ]
subdata$Speices <- factor(subdata$Species)
model1 <- svm(Species ~ Petal.Length + Petal.Width,
data = subdata)
plot(model1, subdata, Petal.Length ~ Petal.Width)
繪制的模型如下:

在使用第一種格式建立模型時(shí),若使用數(shù)據(jù)中的全部特征變量作為模型特征變量時(shí),可以簡要地使用“Species~.”中的“.”代替全部的特征變量。例如下面的代碼就利用了全部四種特征來對三種鳶尾花進(jìn)行分類。
model2 <- svm(Species~., data = iris) summary(model2)
summary函數(shù)的結(jié)果如下:
> model2 <- svm(Species~., data = iris)
> summary(model2)
Call:
svm(formula = Species ~ ., data = iris)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
gamma: 0.25
Number of Support Vectors: 51
( 8 22 21 )
Number of Classes: 3
Levels:
setosa versicolor virginica
通過summary函數(shù)可以得到關(guān)于模型的相關(guān)信息。
- 其中,SVM-Type項(xiàng)目說明本模型的類別為C分類器模型;
- SVM-Kernel項(xiàng)目說明本模型所使用的核函數(shù)為高斯內(nèi)積函數(shù)且核函數(shù)中參數(shù)gamma的取值為0.25;
- cost項(xiàng)目說明本模型確定的約束違反成本為1;
- 此外我們可以看到,模型找到了51個(gè)支持向量:第一類包含有8個(gè)支持向量,第二類包含有22個(gè)支持想想,第三類包含21個(gè)支持向量。
- 最后一行說明模型中的三個(gè)類別分別為setosa、versicolor和virginica。
第二種使用svm()函數(shù)的方式則是根據(jù)所給的數(shù)據(jù)建立模型。這種方式形式要復(fù)雜一些,但是它允許我們以一種更加靈活的方式來構(gòu)建模型。它的函數(shù)使用格式如下(注意我們僅列出了其中的主要參數(shù))。
svm(x, y = NULL, scale = TRUE, type = NULL, kernel = "radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x), coef0 = 0, cost = 1, nu = 0.5, subset, na.action = na.omit)
其中:
- x可以是一個(gè)數(shù)據(jù)矩陣,也可以是一個(gè)數(shù)據(jù)向量,同時(shí)也可以是一個(gè)稀疏矩陣。y是對于x數(shù)據(jù)的結(jié)果標(biāo)簽,它既可以是字符向量也可以為數(shù)值向量。x和y共同決定了將要用來建模的訓(xùn)練數(shù)據(jù)以及模型的積分形式。
- 參數(shù)type用于指定建立模型的類別。支持向量機(jī)模型通常可以用作分類模型、回歸模型和異常檢查模型。根據(jù)用途的不同,在svm函數(shù)中的type可取的值為C-classification、nu-classification、one-classification、eps-regression和nu-regression這五種類型。其中前三種是針對于字符結(jié)果變量的分類方式,其中第三種方式為邏輯判別,即判別結(jié)果輸出所需判別樣本是否屬于該類別。而后兩種則是針對數(shù)值型結(jié)果變量的分類方式。
- kernel是指在模型的建立過程中使用的核函數(shù)。針對線性不可分的問題,為了提高模型預(yù)測精度,通常會只用核函數(shù)對原始數(shù)據(jù)進(jìn)行變換,提高原始特征維度,解決支持向量機(jī)模型線性不可分的問題。svm函數(shù)中kernel參數(shù)有四個(gè)可選核函數(shù),分別為線性核函數(shù)、多項(xiàng)式核函數(shù)、高斯核函數(shù)及神經(jīng)網(wǎng)絡(luò)核函數(shù)。其中,高斯核函數(shù)與多項(xiàng)式核函數(shù)被認(rèn)為是性能最好、也是最常用的核函數(shù)。
核函數(shù)有兩種主要類型:局部性核函數(shù)和全局性核函數(shù),高斯核函數(shù)是一個(gè)典型的局部性核函數(shù),而多項(xiàng)式核函數(shù)則是一個(gè)典型的全局性核函數(shù)。局部性核函數(shù)僅僅在測試點(diǎn)附近小鄰域內(nèi)對數(shù)據(jù)點(diǎn)有影響,其學(xué)習(xí)能力強(qiáng),泛化性能較弱;而全局性核函數(shù)則相對來說泛化性能較強(qiáng),學(xué)習(xí)能力較弱。
- 對于選定的核函數(shù),degree參數(shù)是指核函數(shù)多項(xiàng)式內(nèi)積函數(shù)中的參數(shù),其默認(rèn)值為3。gamma參數(shù)給出了一個(gè)核函數(shù)中除線性內(nèi)積函數(shù)以外的所有函數(shù)的參數(shù),默認(rèn)值為1.coef0參數(shù)是指核函數(shù)中多項(xiàng)式內(nèi)積函數(shù)sigmoid內(nèi)積函數(shù)的中的參數(shù),默認(rèn)值為0.
- 參數(shù)cost是軟間隔模型中離群點(diǎn)權(quán)重。
- 最后,參數(shù)nu是用于nu-regression、nu-classification和one-classification類型中的參數(shù)。
一個(gè)經(jīng)驗(yàn)性的結(jié)論為,在利用svm函數(shù)建立支持向量機(jī)模型時(shí),使用標(biāo)準(zhǔn)化后的數(shù)據(jù)建立的模型效果更好。根據(jù)函數(shù)的第二種使用格式,在針對上述數(shù)據(jù)建立模型時(shí),首先應(yīng)該將結(jié)果變量和特征變量分別提取出來。結(jié)果向量用一個(gè)向量表示,特征向量用一個(gè)矩陣表示。在確定好數(shù)據(jù)后還應(yīng)根據(jù)數(shù)據(jù)分析所使用的核函數(shù)以及核函數(shù)所對應(yīng)的參數(shù)值,通常默認(rèn)使用高斯內(nèi)積函數(shù)作為核函數(shù)。下面給出一段實(shí)例代碼:
# 提取iris數(shù)據(jù)集中除第五列以外的數(shù)據(jù)作為特征變量
x <- iris[, -5]
# 提取iris數(shù)據(jù)集中第五列數(shù)據(jù)作為結(jié)果變量
y <- iris[, 5]
model3 <- svm(x, y, kernel = "radial",
gamma = if (is.vector(x)) 1 else 1 / ncol(x))
在使用第二種格式建立模型時(shí),不需要特別強(qiáng)調(diào)所建立模型的形式,函數(shù)會自動(dòng)將所有輸入的特征變量數(shù)據(jù)作為建立模型所需要的特征向量。在上述過程中,確定核函數(shù)的gamma系數(shù)時(shí)所使用的代碼代表的意思為:如果特征向量是向量則gamma值取1,否則gamma值為特征向量個(gè)數(shù)的倒數(shù)。
在利用樣本數(shù)據(jù)建立模型之后,我們便可以利用模型來進(jìn)行相應(yīng)的預(yù)測和判別。基于svm函數(shù)建立的模型來進(jìn)行預(yù)測時(shí),可以選用函數(shù)predict函數(shù)來完成相應(yīng)的工作。在使用該函數(shù)時(shí),應(yīng)該首先確認(rèn)將要用于預(yù)測的樣本數(shù)據(jù),并將樣本數(shù)據(jù)的特征變量整合后放入同一個(gè)矩陣。代碼如下:
pred <- predict(model3, x) table(pred, y)
輸出結(jié)果:
> pred <- predict(model3, x)
> table(pred, y)
y
pred setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 2
virginica 0 2 48
通常在進(jìn)行預(yù)測之后,還需要檢查模型預(yù)測的準(zhǔn)確程度,這時(shí)便需要使用函數(shù)table來對預(yù)測結(jié)果和真實(shí)結(jié)果做出對比展示。從上述代碼的輸出中,可以看到在模型預(yù)測時(shí),模型將所有屬于setosa類型的鳶尾花全部預(yù)測正確;模型將數(shù)據(jù)versicolor類型的鳶尾花中有48朵預(yù)測正確,另外兩朵錯(cuò)誤的預(yù)測為virginica類型;同樣,模型將屬于virginica類型的鳶尾花中的48朵預(yù)測正確,但也將另外兩朵錯(cuò)誤的預(yù)測為versicolor類型。
函數(shù)predict中的一個(gè)可選參數(shù)是decision.values,在默認(rèn)情況下,該參數(shù)的缺省值為FALSE。若將其值置為TRUE,那么函數(shù)的返回值中將包含有一個(gè)名為decision.values的屬性,該屬性是一個(gè)n*c的矩陣。這里,n是被預(yù)測的數(shù)據(jù)量,c是一個(gè)二分類器的決策值。注意,因?yàn)槲覀兪褂弥С窒蛄繖C(jī)對樣本數(shù)據(jù)進(jìn)行分類,分類結(jié)果可能是有k個(gè)類別。那么這k個(gè)類別中任意兩類之間都會有一個(gè)二分類器。所以,我么可以推斷出總共的二分類器數(shù)量為K(k-1)/2。決策值矩陣中的列名就是二分類器的標(biāo)簽。代碼如下:
pred <- predict(model3, x, decision.values = TRUE) attr(pred, "decision.values")[1:4, ]
輸出如下:
> pred <- predict(model3, x, decision.values = TRUE)
> attr(pred, "decision.values")[1:4, ]
setosa/versicolor setosa/virginica
1 1.196152 1.091757
2 1.064621 1.056185
3 1.180842 1.074542
4 1.110699 1.053012
versicolor/virginica
1 0.6708810
2 0.8483518
3 0.6439798
4 0.6782041
由于我們處理的是一個(gè)分類問題。所以分類決策最終是經(jīng)由一個(gè)sign()函數(shù)來完成的。從上面的輸出中可以看到,對于樣本數(shù)據(jù)4而言,標(biāo)簽setosa/versicolor對應(yīng)的值大于0,因此屬于setosa類;標(biāo)簽setosa/virginica對應(yīng)的值同樣大于0,因此數(shù)據(jù)setosa類;在二分類器versicolor/virginica中對應(yīng)的決策值大于0,判定屬于versicolor類。所以,最終樣本數(shù)據(jù)4被判定數(shù)據(jù)setosa類。
可視化模型,代碼如下:
> plot(cmdscale(dist(iris[,-5])),
+ col=c("orange", "blue", "green")[as.integer(iris[,5])],
+ pch=c("o", "+")[1:150 %in% model3$index + 1])
>
> # ?legend
> legend(1.8, -0.5, c("setosa","versicolor", "virgincia"),
+ col = c("orange","blue","green"), lty = 1,
+ cex = 0.6,
+ bty = "o", box.lty = 1, box.col = "black")

在圖中我們可以看到,鳶尾花中的第一種setosa類別同其他兩種區(qū)別較大,而剩下的versicolor類別和virginica類別卻相差很小,甚至存在交叉難以區(qū)分。注意,這是在使用了全部四種特征之后仍然難以區(qū)分的。這也從另一個(gè)角度解釋了在模型預(yù)測過程中出現(xiàn)的問題,所以模型誤將2朵versicolor 類別的花預(yù)測成了virginica 類別,而將2朵virginica 類別的花錯(cuò)誤地預(yù)測成了versicolor 類別,也就是很正常現(xiàn)象了。
到此這篇關(guān)于R語言實(shí)現(xiàn)支持向量機(jī)SVM應(yīng)用案例的文章就介紹到這了,更多相關(guān)R語言支持向量機(jī)SVM內(nèi)容請搜索服務(wù)器之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持服務(wù)器之家!
原文鏈接:https://blog.csdn.net/yitian_z/article/details/103097463