1. 常用術(shù)語
(1)標(biāo)準(zhǔn)化(Scale)
如果不對(duì)數(shù)據(jù)進(jìn)行scale處理,本身數(shù)值大的基因?qū)χ鞒煞值呢暙I(xiàn)會(huì)大。如果關(guān)注的是變量的相對(duì)大小對(duì)樣品分類的貢獻(xiàn),則應(yīng)SCALE,以防數(shù)值高的變量導(dǎo)入的大方差引入的偏見。但是定標(biāo)(scale)可能會(huì)有一些負(fù)面效果,因?yàn)槎?biāo)后變量之間的權(quán)重就是變得相同。如果我們的變量中有噪音的話,我們就在無形中把噪音和信息的權(quán)重變得相同,但PCA本身無法區(qū)分信號(hào)和噪音。在這樣的情形下,我們就不必做定標(biāo)。
(2)特征值 (eigen value)
特征值與特征向量均為矩陣分解的結(jié)果。特征值表示標(biāo)量部分,一般為某個(gè)主成分的方差,其相對(duì)比例可理解為方差解釋度或貢獻(xiàn)度 ;特征值從第一主成分會(huì)逐漸減小。
(3)特征向量(eigen vector)
特征向量為對(duì)應(yīng)主成分的線性轉(zhuǎn)換向量(線性回歸系數(shù)),特征向量與原始矩陣的矩陣積為主成分得分。特征向量是單位向量,其平方和為1。特征向量主要起轉(zhuǎn)換作用,其數(shù)值不能說明什么問題,解釋力更強(qiáng)的是載荷loadings,但很多R輸出中經(jīng)常混用,engen vector與loadings。
(4)載荷(loading)
因子載荷矩陣并不是主成分的特征向量,即不是主成分的系數(shù)。主成分系數(shù)的求法:各自因子載荷向量除以各自因子特征值的算數(shù)平方根。
- 特征向量是單位向量,特征向量乘以特征值的平方根構(gòu)造了載荷loading。
- 列上看,不同變量對(duì)某一PC的loadings的平方和等于其征值,因此每個(gè)變量的loadings值可表征其對(duì)PC的貢獻(xiàn)。
- 行上看,同一變量對(duì)不同PCs的loadings行平方和為1,表征不同PCs對(duì)某一變量方差的解釋度。
(5)得分(score)
指主成分得分,矩陣與特征向量的積。·
2. PCA分析過程
2.0 手動(dòng)計(jì)算
#特征分解 dat_eigen<-scale(iris[,-5],scale=T)%>%cor()%>%eigen() #特征值提取 dat_eigen$values #特征向量提取 dat_eigen$vectors #求loadings=eigen vector*sqrt(eigen value),與princomp不同 #主成分載荷表示各個(gè)主成分與原始變量的相關(guān)系數(shù)。 sweep(dat_eigen$vectors,2,sqrt(dat_eigen$values),"*") #將中心化的變量矩陣得到每個(gè)觀測(cè)值的得分 scale(iris[,-5],scale=T)%*%dat_eigen$vectors%>%head()
2.1 prcomp函數(shù)
prcomp函數(shù)使用較為簡(jiǎn)單,但是不同于常規(guī)的求取特征值和特征向量的方法,prcomp函數(shù)是對(duì)變量矩陣(相關(guān)矩陣)采用SVD方法計(jì)算其奇異值(原理上是特征值的平方根),函數(shù)幫助中描述為函數(shù)結(jié)果中的sdev。
prcomp函數(shù)輸入?yún)?shù)為變量矩陣(x),中心化(center,默認(rèn)為true),標(biāo)準(zhǔn)化(scale,默認(rèn)為false,建議改為true),主成份個(gè)數(shù)(rank)。
prcomp函數(shù)輸出有sdev(各主成份的奇異值),rotation(特征向量,回歸系數(shù)),x(score得分矩陣)。
iris.pca<-prcomp(iris[,-5],scale=T,rank=4,retx=T) #相關(guān)矩陣分解 #retx表四返回score,scale表示要標(biāo)準(zhǔn)化 summary(iris.pca) #方差解釋度 iris.pca$sdev #特征值的開方 iris.pca$rotation #特征向量,回歸系數(shù) iris.pca$x #樣本得分score
2.2 princomp函數(shù)
princomp以計(jì)算相關(guān)矩陣或者協(xié)方差矩陣的特征值為主要手段。
princomp函數(shù)輸出有主成份的sd,loading,score,center,scale.
prcomp函數(shù)使用較為簡(jiǎn)單,但是不同于常規(guī)的求取特征值和特征向量的方法,prcomp函數(shù)是對(duì)變量矩陣(相關(guān)矩陣)采用SVD方法計(jì)算其奇異值(原理上是特征值的平方根),函數(shù)幫助中描述為函數(shù)結(jié)果中的sdev。
prcomp函數(shù)輸入?yún)?shù)為變量矩陣(x),中心化(center,默認(rèn)為true),標(biāo)準(zhǔn)化(scale,默認(rèn)為false,建議改為true),主成份個(gè)數(shù)(rank)。
prcomp函數(shù)輸出有sdev(各主成份的奇異值及其方差累積),rotation(載荷矩陣),x(得分矩陣),center(變量的均值),scale(變量的標(biāo)準(zhǔn)偏差)
data(wine) #三種葡萄釀造的紅酒品質(zhì)分析數(shù)據(jù)集 wine.pca<-princomp(wine,cor=T,scores=T) #默認(rèn)方差矩陣(cor=F),改為cor=T則結(jié)果與prcomp相同 summary(wine.pca) #各主成份的SVD值以及相對(duì)方差 wine.pca$loading #特征向量,回歸系數(shù) wine.pca$score screenplot(wine.pca) #方差分布圖 biplot(wine.pca,scale=F) #碎石圖,直接把x與rotation繪圖,而不標(biāo)準(zhǔn)化
2.3 psych::principal
實(shí)際上該principal主要用于因子分析。
model_pca<-psych::principal(iris[,-5],nfactors=4,rotate="none") model_pca$values # 特征值=sdev^2 # 此處loadings與手動(dòng)計(jì)算相同=prcomp的rotation*sdev model_pca%>%.$loadings #載荷,不是特征向量 #此處score=prcomp的score/sdev model_pca$scores[1:5,] #此處為因子得分,不是主成分得分 model_pca$weights #此處為上面loadings/特征值,也稱成份得分系數(shù)或者因子系數(shù)
3. PCA結(jié)果解釋
下文引用chentong的內(nèi)容
prcomp函數(shù)會(huì)返回主成分的標(biāo)準(zhǔn)差、特征向量和主成分構(gòu)成的新矩陣。 不同主成分對(duì)數(shù)據(jù)差異的貢獻(xiàn)和主成分與原始變量的關(guān)系。 1. 主成分的平方為為特征值,其含義為每個(gè)主成分可以解釋的數(shù)據(jù)差異,計(jì)算方式為 eigenvalues = (pca$sdev)^2 2. 每個(gè)主成分可以解釋的數(shù)據(jù)差異的比例為 percent_var = eigenvalues*100/sum(eigenvalues) 3. 可以使用summary(pca)獲取以上兩條信息。 這兩個(gè)信息可以判斷主成分分析的質(zhì)量: 成功的降維需要保證在前幾個(gè)為數(shù)不多的主成分對(duì)數(shù)據(jù)差異的解釋可以達(dá)到80-90%。 指導(dǎo)選擇主成分的數(shù)目: 1. 選擇的主成分足以解釋的總方差大于80% (方差比例碎石圖) 2. 從前面的協(xié)方差矩陣可以看到,自動(dòng)定標(biāo)(scale)的變量的方差為1 (協(xié)方差矩陣對(duì)角線的值)。待選擇的主成分應(yīng)該是那些方差大于1的主成分,即其解釋的方差大于原始變量(特征值碎石圖,方差大于1,特征值也會(huì)大于1,反之亦然)。 鑒定核心變量和變量間的隱性關(guān)系: 原始變量與主成分的相關(guān)性 Variable correlation with PCs (var.cor) = loadings * sdev 原始數(shù)據(jù)對(duì)主成分的貢獻(xiàn)度 var.cor^2 / (total var.cor^2)
4. PCA結(jié)果可視化
4.1 ggbiplot包
devtools::install_github("vqv/ggbiplot")
library(ggbiplot)
ggscreeplot(wine.pca) #碎石圖
碎石圖

biplot
ggbiplot(wine.pca, obs.scale = 1, var.scale = 1, groups = wine.class, ellipse = TRUE, circle = TRUE) + scale_color_discrete(name = '') + theme(legend.direction = 'horizontal', legend.position = 'top')

4.2 ggfortify包
ggfortify包中autoplot函數(shù)可自動(dòng)繪制。
library(ggfortify) pca1<-iris%>%select(-5)%>%prcomp() autoplot(pca1,data = iris,col= 'Species',size=2, loadings =T,loadings.label = TRUE, frame = TRUE,frame.type='norm', label = TRUE, label.size = 3 )+ theme_classic()

4.3 factoextra包可視化
FactoMineR與factoextra分別進(jìn)行PCA分析與可視化,當(dāng)然factoextra包中函數(shù)也可對(duì)prcomp、princomp函數(shù)結(jié)果進(jìn)行可視化。
library(factoextra) library(FactoMineR) # 利用FactoMineR包中PCA函數(shù)進(jìn)行PCA分析 > wine.pca2 <- PCA(wine,scale.unit = T,ncp=5,graph = T) #
wine.pca2中內(nèi)容
> print(wine.pca2) **Results for the Principal Component Analysis (PCA)** The analysis was performed on 178 individuals, described by 13 variables *The results are available in the following objects: name description 1 "$eig" "eigenvalues" 2 "$var" "results for the variables" 3 "$var$coord" "coord. for the variables" 4 "$var$cor" "correlations variables - dimensions" 5 "$var$cos2" "cos2 for the variables" 6 "$var$contrib" "contributions of the variables" 7 "$ind" "results for the individuals" 8 "$ind$coord" "coord. for the individuals" 9 "$ind$cos2" "cos2 for the individuals" 10 "$ind$contrib" "contributions of the individuals" 11 "$call" "summary statistics" 12 "$call$centre" "mean of the variables" 13 "$call$ecart.type" "standard error of the variables" 14 "$call$row.w" "weights for the individuals" 15 "$call$col.w" "weights for the variables"
摘要信息
> summary(wine.pca2)
Call:
PCA(X = wine, scale.unit = T, ncp = 5, graph = T)
Eigenvalues
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8 Dim.9 Dim.10
Variance 4.706 2.497 1.446 0.919 0.853 0.642 0.551 0.348 0.289 0.251
% of var. 36.199 19.207 11.124 7.069 6.563 4.936 4.239 2.681 2.222 1.930
Cumulative % of var. 36.199 55.406 66.530 73.599 80.162 85.098 89.337 92.018 94.240 96.170
Dim.11 Dim.12 Dim.13
Variance 0.226 0.169 0.103
% of var. 1.737 1.298 0.795
Cumulative % of var. 97.907 99.205 100.000
...省略...
還輸出了簡(jiǎn)易的圖

4.3.1 特征值可視化 提取特征值
> get_eigenvalue(wine.pca2) #標(biāo)準(zhǔn)化數(shù)據(jù)中特征值>1的變量解釋能力較強(qiáng) eigenvalue variance.percent cumulative.variance.percent Dim.1 4.7058503 36.1988481 36.19885 Dim.2 2.4969737 19.2074903 55.40634 Dim.3 1.4460720 11.1236305 66.52997 ...省略部分
碎石圖
fviz_eig(wine.pca2,addlabels = TRUE) #碎石圖,展示方差解釋度

4.3.2 變量信息可視化
變量提取主要有g(shù)et_pca_var()函數(shù),輸出變量在主成分投影上的坐標(biāo),變量與主成分PC的相關(guān)系數(shù),相關(guān)系數(shù)的平方,變量對(duì)某一PC的相關(guān)貢獻(xiàn)
#get_pca_var()等同于get_pca(element="var") > get_pca_var(wine.pca2)#coord cor cos2 contribution Principal Component Analysis Results for variables =================================================== Name Description 1 "$coord" "Coordinates for the variables" 2 "$cor" "Correlations between variables and dimensions" 3 "$cos2" "Cos2 for the variables" 4 "$contrib" "contributions of the variables" > wine.pca2$var #輸出上述數(shù)據(jù) > get_pca_var(wine.pca2)$coord > get_pca_var(wine.pca2)$cos2
變量坐標(biāo)(coord)與相關(guān)性(cor)可視化
coord是坐標(biāo)(實(shí)際的loading),與cor數(shù)值相同
coord=eigen vector * stdev
相關(guān)圖中,靠近的變量表示正相關(guān);對(duì)向的是負(fù)相關(guān)。
箭頭越遠(yuǎn)離遠(yuǎn)原點(diǎn)、越靠經(jīng)圓圈表明PC對(duì)其的代表性高(相關(guān)性強(qiáng))
fviz_pca_var(wine.pca2) #變量相關(guān)性可視化圖

cos2可視化
cos2代表不同主成分對(duì)變量的代表性強(qiáng)弱,對(duì)特定變量,所有組成份上的cos2之和為1,因?yàn)閏os2為cor的平方,所以也認(rèn)為是相關(guān)性越強(qiáng),其結(jié)果與cor類似。
#cos2是coord的平方,表征特定變量在所有PC上的代表性,某個(gè)變量的所有cos2總和為1
library("corrplot")
corrplot(get_pca_var(wine.pca2)$cos2, is.corr=FALSE)
下圖中PC1對(duì)Phenols變量的代表性最好

fviz_cos2(wine.pca2, choice = "var", axes = 1:2) # cos2在主成分上的加和,并排序

#不同按照cos2大小設(shè)定顏色梯度,也可以設(shè)置alpha梯度
fviz_pca_var(wine.pca2,axes=c(1,2),
col.var = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE) # Avoid text overlapping

contrib可視化
contrib是每個(gè)變量對(duì)某一特定PC的貢獻(xiàn)
contrib=(var.cos2 * 100) / (total cos2 of the PC component)
多個(gè)變量的contrib = [(Contrb1 * Eig1) + (Contrib2 * Eig2)]/(Eig1 + Eig2)
> get_pca_var(wine.pca2)$contrib
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
Alcohol 2.083097e+00 23.391881971 4.3007553 0.03188475 7.0577176
MalicAcid 6.011695e+00 5.059392535 0.7923294 28.82511766 0.1240000
Ash 4.206853e-04 9.989949520 39.2156374 4.58711714 2.0456286
AlcAsh 5.727426e+00 0.011215874 37.4642355 0.37038683 0.4369599
Mg 2.016174e+00 8.978053590 1.7097376 12.37608338 52.8599543
Phenols 1.557572e+01 0.423013810 2.1368289 3.92310704 2.2295987
Flav 1.788734e+01 0.001128834 2.2705035 2.31937045 1.1886633
NonFlavPhenols 8.912201e+00 0.082825894 2.9025311 4.13313047 25.0703477
Proa 9.823804e+00 0.154462537 2.2336591 15.92461164 1.8730611
Color 7.852920e-01 28.089541241 1.8852996 0.43461955 0.5842581
Hue 8.803953e+00 7.797226784 0.7262776 18.29883787 3.0142002
OD 1.415019e+01 2.705899746 2.7557523 3.39004479 1.0233546
Proline 8.222684e+00 13.315407665 1.6064528 5.38568842 2.4922558
fviz_contrib(wine.pca2, choice = "var", axes = 1:2)
corrplot(get_pca_var(wine.pca2)$contrib, is.corr=FALSE)

fviz_contrib(wine.pca2, choice = "var", axes = 1:2)

根據(jù)contribution將變量顏色分類
fviz_pca_var(wine.pca2,col.var = "contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"))

變量分組
#人為分組
bb<-as.factor(c(rep(c("soil","micro","plant"),4),"soil"))
names(bb)<-row.names(wine.pca2$var$contrib)
fviz_pca_var(wine.pca2, col.var = bb, palette = c("#0073C2FF", "#EFC000FF", "#868686FF"),
legend.title = "Cluster")

4.3.3 樣本可視化scores 樣本坐標(biāo)可視化
get_pca_ind(wine.pca2) #coord cor cos2 contribution
get_pca(element="ind)
get_pca_ind(wine.pca2) #coord cor cos2 contribution wine.pca2$ind #coord cos2 contrib dist fviz_pca_ind(wine.pca2)#score 可視化coord

fviz_pca_ind(wine.pca2, geom=c("point","text"),
addEllipses = T,
pointshape=21,col.ind="black",pointsize="cos2",
fill.ind = wine.class,palette = "npg",
#col.ind="cos2", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
#col.ind="contrib", gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
# label=wine.class,
repel = TRUE)

fviz_pca_ind(wine.pca2, axes = c(1, 2),label="none", #habillage只能是分類變量
addEllipses = TRUE, ellipse.type="norm",ellipse.level=0.9,
# one of "confidence","t","norm","euclid","convex"
habillage = wine.class,palette = "jco",
mean.point=F
)

樣本的cos2與contrib圖
fviz_cos2(wine.pca2, choice = "ind",axes=1:2)

fviz_contrib(wine.pca2, choice = "ind", axes = 1:2)

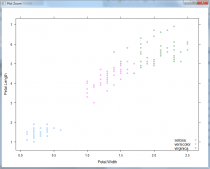
4.3.4 biplot
biplot不需要關(guān)注具體數(shù)值,只需要關(guān)注方向與位置
樣本在變量同側(cè)是具有高數(shù)值,反之則值低
fviz_pca_biplot(wine.pca2, axes = c(1,2),repel = F,
addEllipses = T,ellipse.alpha=0.15,
geom=c("point"),geom.var=c("arrow","text"),
arrowsize=1.5,labelsize=5, #arrow與text大小
pointshape=21,pointsize=5,fill.ind = wine.class,col.ind="black", #point
col.var=factor(c(rep(c("soil","plant"),6),"plant"))
)%>%ggpar(xlab="PC1",ylab="PC2",title="PCA-Biplot",
font.x=14,font.y=14,font.tickslab = 14,ggtheme=theme_bw(),ylim=c(-4.5,4.5),
legend.title = list(color="Variable",fill="Class"),font.legend = 12,
)+
ggpubr::fill_palette("jco")+ggpubr::color_palette("npg")+
theme(axis.ticks.length= unit(-0.25, 'cm'), #設(shè)置y軸的刻度長(zhǎng)度為負(fù)數(shù),即向內(nèi)
axis.text.y.left = element_text(margin = unit(c(0.5, 0.5, 0.5, 0.05), 'cm')),
axis.text.x.bottom = element_text(margin = unit(c(0.5, 0.5, 0.05, 0.5), 'cm'))
)

到此這篇關(guān)于詳解R語言中的PCA分析與可視化的文章就介紹到這了,更多相關(guān)R語言PCA分析與可視化內(nèi)容請(qǐng)搜索服務(wù)器之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持服務(wù)器之家!
原文鏈接:https://blog.csdn.net/nikang3148/article/details/85246555