訓練深層神經(jīng)網(wǎng)絡是十分困難的，特別是在較短的實踐內(nèi)使他們收斂更加棘手。在本節(jié)中，我們將介紹批量歸一化（batch normalization），這是一種流行且有效的技術(shù)，可持續(xù)加速深層網(wǎng)絡的收斂速度。在結(jié)合之后將介紹的殘差快，批量歸一化使得研究人員能夠訓練100層以上的網(wǎng)絡。

訓練深層網(wǎng)絡

為什么要批量歸一化層呢？

讓我們回顧一下訓練神經(jīng)網(wǎng)絡時出現(xiàn)的一些實際挑戰(zhàn)：

1.數(shù)據(jù)預處理的方式通常會對最終結(jié)果產(chǎn)生巨大影響。回想一下我們應用多層感知機來預測房價的例子。使用真實數(shù)據(jù)時，我們的第一步是標準化輸入特征，使其平均值為0，方差為1。直觀地說，這種標準化可以很好地與我們地優(yōu)化器配合使用，因為它可以將參數(shù)的量級進行統(tǒng)一。

2.對于典型的多層感知機或卷積伸進網(wǎng)絡。當我們訓練時，中間層中的變量（例如，多層感知機中的仿射變換輸出）可能具有更廣的變化范圍：不論是沿著從輸入到輸出的層，跨同一層中的單元，或是隨著時間的推移，模型的參數(shù)隨著訓練更新變幻莫測。批量歸一化的發(fā)明者非正式地假設，這些變量分布中的這種偏移可能會阻礙網(wǎng)絡的收斂。直觀地說，我們可能會猜想，如果一個層的可變值是另一層的100倍，這可能需要對學習率進行補償調(diào)整。

3.更深層的網(wǎng)絡很復雜，容易過擬合。這意味著正則化變得更加需要。

批量歸一化應用于單個可選層（也可以應用到所有層），其原理如下：
在每次訓練迭代中，我們首先歸一化輸入，即通過減去其平均值并除以其標準差，其中兩者均基于當前小批量處理。
接下來，我們應用比例系數(shù)和比例偏移。
正是由于這個基于批量統(tǒng)計的標準化，才有了批量標準化的名稱。

這里，如果我們嘗試使用大小為1的小批量應用小批量歸一化，我們將無法學到任何東西。這是因為在減去均值之后，每個隱藏單元將為0。所以，只有使用足夠大的小批量，批量歸一化這種方法才是有效且穩(wěn)定的。請注意，在應用批量歸一化時，批量大小的選擇可能比沒有批量歸一化時更重要。

現(xiàn)在，我們了解一下批量歸一化在實踐中是如何工作的。

批量歸一化層

回想一下，批量歸一化和其他圖層之間的一個關鍵區(qū)別是，由于批量歸一化在完整的小批次上運行，因此我們不能像以前在引入其他圖層時忽略批處理的尺寸大小。我們在下面討論這兩種情況：全連接層和卷積層，它們的批量歸一化實現(xiàn)略有不同。

全連接層

通常，我們將批量歸一化層置于全連接層中的仿射變換和激活函數(shù)之間。

卷積層

同樣，對于卷積層，我們可以在卷積層之后和非線性激活函數(shù)之前應用批量歸一化。當卷積有多個輸出通道時，我們需要對這些通道的“每個”輸出執(zhí)行批量歸一化，每個用到都有自己的拉伸和偏移參數(shù)，這兩個參數(shù)都是標量。假設我們的微批次包含 m m m個示例，并且對于每個通道，卷積的輸出具有高度 p p p和寬度 q q q。那么對于卷積層，我們在每個輸出通道的 m ∗ p ∗ q m*p*q m∗p∗q個元素上同時執(zhí)行每個批量歸一化。因此，在計算平均值和方差時，我們會收集所有空間位置的值，然后在給定通道內(nèi)應用相同的均值和方差，以便在每個空間位置對值進行歸一化。

預測過程中的批量歸一化

正如我們前面提到的，批量歸一化在訓練模式和預測模式下的行為通常是不同的。
首先，將訓練好的模型用于預測時，我們不再需要樣本均值中的噪聲以及在微批次上估計每個小批次產(chǎn)生的樣本方差了。
其次，例如，我們可能需要使用我們的模型對逐個樣本進行預測。一種常用的方法是通過移動平均估算整個訓練數(shù)據(jù)集的樣本均值和方差，并在預測時使用它們得到確定的輸出。可見，和dropout一樣，批量歸一化層在訓練模式和預測模式下的計算結(jié)果也是不一樣的。

使用批量歸一化層的LeNet

為了更好理解如何應用BatchNorm，下面我們將其應用于LeNet模型。回想一下，批量歸一化是在卷積層或全連接層之后、相應的激活函數(shù)之前應用的。

net = nn.Sequential(
	nn.Conv2d(1, 6, kernel_size = 5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
	nn.MaxPool2d(kernel_size=2, stride=2)
	nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
	nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
	nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
	nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
	nn.Linear(84, 10)
)

和以前一樣，我們將在Fashion-MNIST數(shù)據(jù)集上訓練網(wǎng)絡。這個代碼與我們第一次訓練LeNet時幾乎完全相同，主要區(qū)別在于學習率大得多。

lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.250, train acc 0.907, test acc 0.801
35560.7 examples/sec on cuda:0

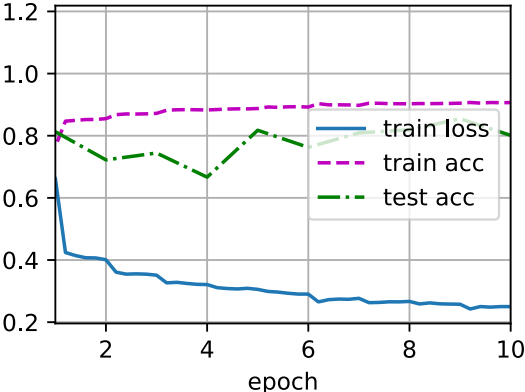
讓我們來看看從第一個批量歸一化層中學到的拉伸參數(shù)gamma和便宜參數(shù)beta。

net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

(tensor([0.7562, 1.2784, 2.3527, 1.3189, 2.0457, 2.8424], device='cuda:0',
grad_fn=<ViewBackward>),
tensor([ 0.7436, -0.8156, -0.2711, -0.5087, 0.5847, -3.0033], device='cuda:0',
grad_fn=<ViewBackward>))

簡明實現(xiàn)

除了使用我們剛剛定義的BatchNorm，我們也可以直接使用深度學習框架中定義的BatchNorm。該代碼看起來幾乎與我們上面的代碼相同。

net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
nn.Linear(84, 10))

下面，我們使用相同超參數(shù)來訓練模型。請注意，通常高級API變體運行速度快得多，因為它的代碼已編譯為C++或CUDA，而我們自定義代碼由Python實現(xiàn)。

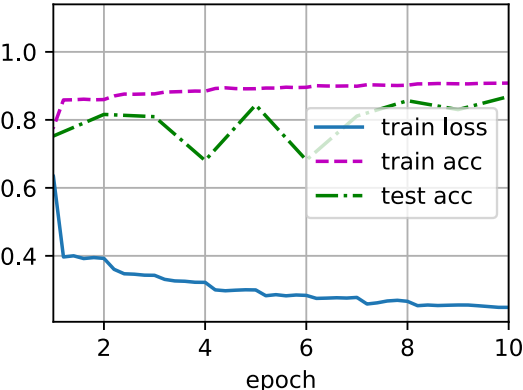
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.248, train acc 0.908, test acc 0.869
60219.9 examples/sec on cuda:0

爭議

直觀地說，批量歸一化被認為可以使優(yōu)化更加平滑。

然而，在提出批量歸一化的論文中，作者除了介紹了其應用，還解釋了其原理：通過減少內(nèi)部協(xié)變量。然而這種解釋更偏向于個人直覺。

但是批量歸一化的效果很好，它適用于幾乎所有圖像分類器，并在學術(shù)界獲得了數(shù)萬引用。

以上就是Python深度學習理解pytorch神經(jīng)網(wǎng)絡批量歸一化的詳細內(nèi)容，更多關于pytorch神經(jīng)網(wǎng)絡批量歸一化的資料請關注服務器之家其它相關文章！

原文鏈接：https://blog.csdn.net/weixin_43880225/article/details/120626891?spm=1001.2014.3001.5501