對于想深入了解線性回歸的童鞋,這里給出一個完整的例子,詳細學完這個例子,對用scikit-learn來運行線性回歸,評估模型不會有什么問題了。
1. 獲取數據,定義問題
沒有數據,當然沒法研究機器學習啦。:) 這里我們用uci大學公開的機器學習數據來跑線性回歸。
數據的介紹在這:http://archive.ics.uci.edu/ml/datasets/Combined+Cycle+Power+Plant
數據的下載地址在這:http://archive.ics.uci.edu/ml/machine-learning-databases/00294/
里面是一個循環發電場的數據,共有9568個樣本數據,每個數據有5列,分別是:at(溫度), v(壓力), ap(濕度), rh(壓強), pe(輸出電力)。我們不用糾結于每項具體的意思。
我們的問題是得到一個線性的關系,對應pe是樣本輸出,而at/v/ap/rh這4個是樣本特征, 機器學習的目的就是得到一個線性回歸模型,即:
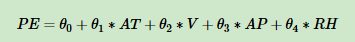
pe=θ 0 +θ 1 ∗at+θ 2 ∗v+θ 3 ∗ap+θ 4 ∗rh 而需要學習的,就是\(\theta_0, \theta_1, \theta_2, \theta_3, \theta_4\)這5個參數。
2. 整理數據
下載后的數據可以發現是一個壓縮文件,解壓后可以看到里面有一個xlsx文件,我們先用excel把它打開,接著“另存為“”csv格式,保存下來,后面我們就用這個csv來運行線性回歸。
打開這個csv可以發現數據已經整理好,沒有非法數據,因此不需要做預處理。但是這些數據并沒有歸一化,也就是轉化為均值0,方差1的格式。也不用我們搞,后面scikit-learn在線性回歸時會先幫我們把歸一化搞定。
好了,有了這個csv格式的數據,我們就可以大干一場了。
3.用pandas來讀取數據
我們先打開ipython notebook,新建一個notebook。當然也可以直接在python的交互式命令行里面輸入,不過還是推薦用notebook。下面的例子和輸出我都是在notebook里面跑的。
先把要導入的庫聲明了:
|
1
2
3
4
5
|
import matplotlib.pyplot as plt%matplotlib inlineimport numpy as npimport pandas as pdfrom sklearn import datasets, linear_model |
接著我們就可以用pandas讀取數據了:
|
1
2
|
# read_csv里面的參數是csv在你電腦上的路徑,此處csv文件放在notebook運行目錄下面的ccpp目錄里data = pd.read_csv('.\ccpp\ccpp.csv') |
測試下讀取數據是否成功:
|
1
2
|
#讀取前五行數據,如果是最后五行,用data.tail()data.head() |
運行結果應該如下,看到下面的數據,說明pandas讀取數據成功:
| at | v | ap | rh | pe | |
|---|---|---|---|---|---|
| 0 | 8.34 | 40.77 | 1010.84 | 90.01 | 480.48 |
| 1 | 23.64 | 58.49 | 1011.40 | 74.20 | 445.75 |
| 2 | 29.74 | 56.90 | 1007.15 | 41.91 | 438.76 |
| 3 | 19.07 | 49.69 | 1007.22 | 76.79 | 453.09 |
| 4 | 11.80 | 40.66 | 1017.13 | 97.20 | 464.43 |
4.準備運行算法的數據
我們看看數據的維度:
|
1
|
data.shape |
結果是(9568, 5)。說明我們有9568個樣本,每個樣本有5列。
現在我們開始準備樣本特征x,我們用at, v,ap和rh這4個列作為樣本特征。
|
1
2
|
x = data[['at', 'v', 'ap', 'rh']]x.head() |
可以看到x的前五條輸出如下:
| at | v | ap | rh | |
|---|---|---|---|---|
| 0 | 8.34 | 40.77 | 1010.84 | 90.01 |
| 1 | 23.64 | 58.49 | 1011.40 | 74.20 |
| 2 | 29.74 | 56.90 | 1007.15 | 41.91 |
| 3 | 19.07 | 49.69 | 1007.22 | 76.79 |
| 4 | 11.80 | 40.66 | 1017.13 | 97.20 |
接著我們準備樣本輸出y, 我們用pe作為樣本輸出。
|
1
2
|
y = data[['pe']]y.head() |
可以看到y的前五條輸出如下:
| pe | |
|---|---|
| 0 | 480.48 |
| 1 | 445.75 |
| 2 | 438.76 |
| 3 | 453.09 |
| 4 | 464.43 |
5. 劃分訓練集和測試集
我們把x和y的樣本組合劃分成兩部分,一部分是訓練集,一部分是測試集,代碼如下:
|
1
2
|
from sklearn.cross_validation import train_test_splitx_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1) |
查看下訓練集和測試集的維度:
|
1
2
3
4
|
print x_train.shapeprint y_train.shapeprint x_test.shapeprint y_test.shape |
結果如下:
(7176, 4)
(7176, 1)
(2392, 4)
(2392, 1)
可以看到75%的樣本數據被作為訓練集,25%的樣本被作為測試集。
6. 運行scikit-learn的線性模型
終于到了臨門一腳了,我們可以用scikit-learn的線性模型來擬合我們的問題了。scikit-learn的線性回歸算法使用的是最小二乘法來實現的。代碼如下:
|
1
2
3
|
from sklearn.linear_model import linearregressionlinreg = linearregression()linreg.fit(x_train, y_train) |
擬合完畢后,我們看看我們的需要的模型系數結果:
|
1
2
|
print linreg.intercept_print linreg.coef_ |
輸出如下:
[ 447.06297099]
[[-1.97376045 -0.23229086 0.0693515 -0.15806957]]
這樣我們就得到了在步驟1里面需要求得的5個值。也就是說pe和其他4個變量的關系如下:

7. 模型評價
我們需要評估我們的模型的好壞程度,對于線性回歸來說,我們一般用均方差(mean squared error, mse)或者均方根差(root mean squared error, rmse)在測試集上的表現來評價模型的好壞。
我們看看我們的模型的mse和rmse,代碼如下:
|
1
2
3
4
5
6
7
|
#模型擬合測試集y_pred = linreg.predict(x_test)from sklearn import metrics# 用scikit-learn計算mseprint "mse:",metrics.mean_squared_error(y_test, y_pred)# 用scikit-learn計算rmseprint "rmse:",np.sqrt(metrics.mean_squared_error(y_test, y_pred)) |
輸出如下:
mse: 20.0804012021
rmse: 4.48111606657
得到了mse或者rmse,如果我們用其他方法得到了不同的系數,需要選擇模型時,就用mse小的時候對應的參數。
比如這次我們用at, v,ap這3個列作為樣本特征。不要rh, 輸出仍然是pe。代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
x = data[['at', 'v', 'ap']]y = data[['pe']]x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1)from sklearn.linear_model import linearregressionlinreg = linearregression()linreg.fit(x_train, y_train)#模型擬合測試集y_pred = linreg.predict(x_test)from sklearn import metrics# 用scikit-learn計算mseprint "mse:",metrics.mean_squared_error(y_test, y_pred)# 用scikit-learn計算rmseprint "rmse:",np.sqrt(metrics.mean_squared_error(y_test, y_pred)) |
輸出如下:
mse: 23.2089074701
rmse: 4.81756239919
可以看出,去掉rh后,模型擬合的沒有加上rh的好,mse變大了。
8. 交叉驗證
我們可以通過交叉驗證來持續優化模型,代碼如下,我們采用10折交叉驗證,即cross_val_predict中的cv參數為10:
|
1
2
3
4
5
6
7
8
|
x = data[['at', 'v', 'ap', 'rh']]y = data[['pe']]from sklearn.model_selection import cross_val_predictpredicted = cross_val_predict(linreg, x, y, cv=10)# 用scikit-learn計算mseprint "mse:",metrics.mean_squared_error(y, predicted)# 用scikit-learn計算rmseprint "rmse:",np.sqrt(metrics.mean_squared_error(y, predicted)) |
輸出如下:
mse: 20.7955974619
rmse: 4.56021901469
可以看出,采用交叉驗證模型的mse比第6節的大,主要原因是我們這里是對所有折的樣本做測試集對應的預測值的mse,而第6節僅僅對25%的測試集做了mse。兩者的先決條件并不同。
9. 畫圖觀察結果
這里畫圖真實值和預測值的變化關系,離中間的直線y=x直接越近的點代表預測損失越低。代碼如下:
|
1
2
3
4
5
6
|
fig, ax = plt.subplots()ax.scatter(y, predicted)ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)ax.set_xlabel('measured')ax.set_ylabel('predicted')plt.show() |
輸出的圖像如下:
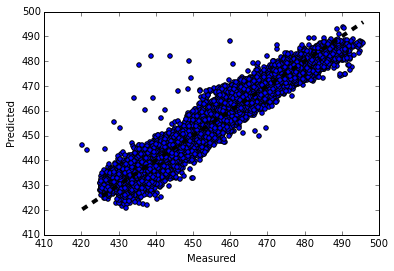
完整的jupyter-notebook代碼參看我的github。
以上就是用scikit-learn和pandas學習線性回歸的過程,希望可以對初學者有所幫助。也希望大家多多支持服務器之家。
原文鏈接:https://www.cnblogs.com/pinard/p/6016029.html










