国产片侵犯亲女视频播放_亚洲精品二区_在线免费国产视频_欧美精品一区二区三区在线_少妇久久久_在线观看av不卡

服務器之家：專注于服務器技術及軟件下載分享
分類導航

PHP教程|ASP.NET教程|Java教程|ASP教程|編程技術|正則表達式|C/C++|IOS|C#|Swift|Android|VB|R語言|JavaScript|易語言|vb.net|

服務器之家 - 編程語言 - C/C++ - 數據結構 紅黑樹的詳解

數據結構 紅黑樹的詳解

2021-05-25 13:35xiaohusaier C/C++

這篇文章主要介紹了數據結構 紅黑樹的詳解的相關資料,數據結構中的二叉樹查找，紅黑樹的講解，需要的朋友可以參考下

數據結構 紅黑樹的詳解

紅黑樹是具有下列著色性質的二叉查找樹：

1.每一個節點或者著紅色，或者著黑色。

2.根是黑色的。

3.如果一個節點是紅色的，那么它的子節點必須是黑色。

4.從一個節點到一個NULL指針的每一條路徑必須包含相同數目的黑色節點。

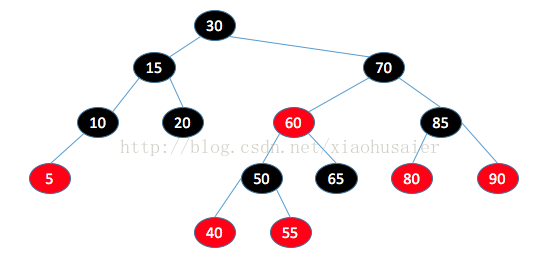
下面是一棵紅黑樹。

數據結構 紅黑樹的詳解

 

1.自底向上插入

通常把新項作為樹葉放到樹中。如果我們把該項涂成黑色，那么違反條件4，因為將會建立一條更長的黑節點路徑。因此這一項必須涂成紅色。如果它的父節點是黑色的，插入完成。如果父節點是紅色的，那么違反條件3。在這種情況下我們必須調整該樹以滿足條件3。用于完成這項目任務的基本操作是顏色的改變和樹的旋轉。

如果新插入的節點的父節點是黑色，那么插入完成。

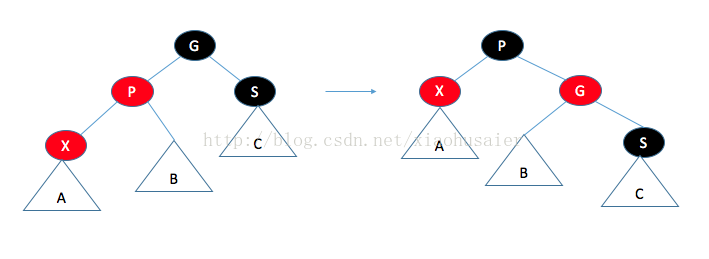
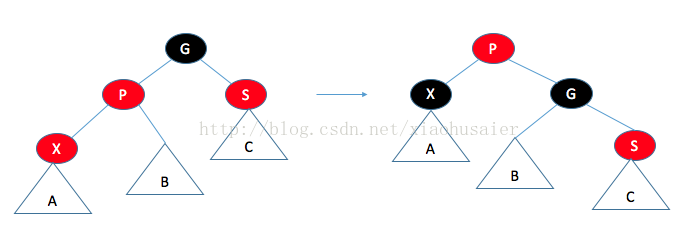
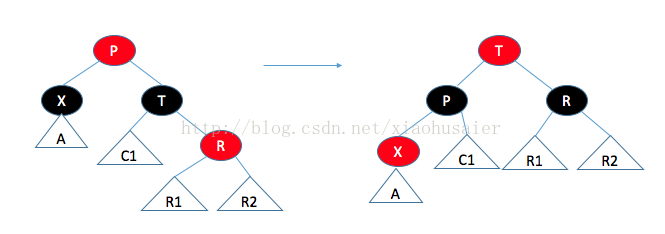
如果父節點是紅色，那么有幾種情形需要考慮。首先，假設這個父節點的兄弟是黑色（NULL節點約定為黑色）。這對于插入3或8是適用的，但對插入99不適用。令X是新加的樹葉，P是它的父節點，S是該父節點的兄弟，G是祖父節點情況一：父節點的兄弟是黑色的。通過操作使得到達A,B,C的黑色路徑保持不變（滿足條件4），而且沒有連續的紅色節點（滿足條件3）.。

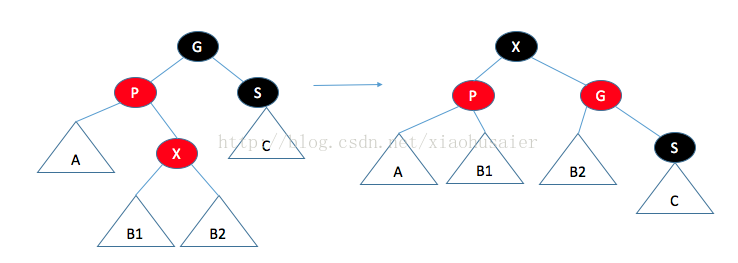
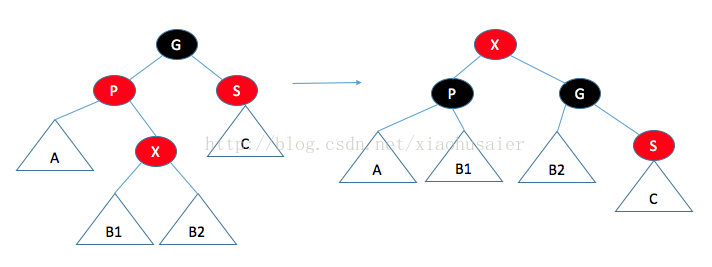
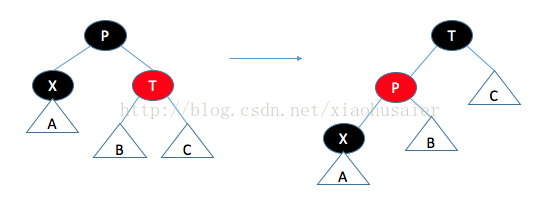
數據結構 紅黑樹的詳解

數據結構 紅黑樹的詳解

 

情況二：父節點的兄弟是紅色的。

 

數據結構 紅黑樹的詳解

 

數據結構 紅黑樹的詳解

 

2.自頂向下刪除

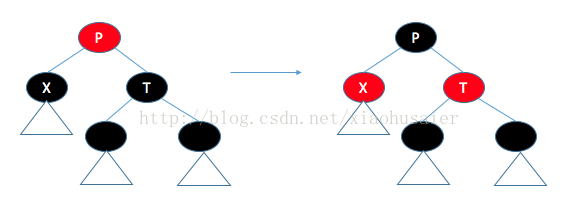
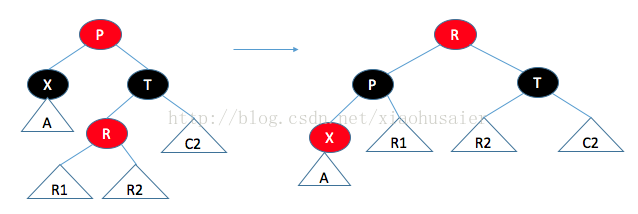
紅黑樹中的刪除可以是自頂向下進行。每一件工作都歸結于能夠刪除一片樹葉。這是因為，要刪除一個帶有兩個兒子的節點，我們用右子樹上的最小節點代替它；該節點最多有一個兒子，然后將該節點刪除。只有一個右兒子的節點可以用相同的方式刪除，而只有一個左兒子的節點通過用其左子樹上最大的節點替換，然后可將該節點刪除。但是假如刪除的節點不是紅色的，那么就會破壞紅黑樹的平衡。解決的方法就是保證從上到下刪除期間樹葉是紅色的。

在整個討論中，令X為當前節點，T是它的兄弟，而P是它們的父親。開始時我們把根涂成紅色。當沿著樹向下遍歷時，我們設法保證X是紅色的。當我們到達一個新的節點時，我們要確信P是紅色的并且X和T是黑色的（因為不能有兩個相連的紅色節點）。存在兩種主要情形。
情況一：X有兩個黑色兒子。此時有三個子情況。
（1）T有兩個黑兒子，那么我們可以翻轉X、T、P的顏色來保持這種不變性。
數據結構 紅黑樹的詳解
（2）T的左兒子是紅色的
數據結構 紅黑樹的詳解
（3）T的右兒子是紅色的
數據結構 紅黑樹的詳解
情況二：X的兒子之一是紅的。在這種情況下，我們落到下一層，得到新的X、T、P。如果幸運，X落在紅兒子上。則我們繼續前行。如果不是這樣，那么我們知道T將是紅的，而X和P將是黑的。我們可以旋轉T和P，使得X的新父親是紅的；當然X和它的祖父是黑的。此時我們可以回到第一種主情況。
數據結構 紅黑樹的詳解
3.紅黑樹的實現
3.1 頭文件
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//
// RedBlackTree.h
// RedBlackTree3
//
// Created by Wuyixin on 2017/7/3.
// Copyright © 2017年 Coding365. All rights reserved.
//
 
#ifndef RedBlackTree_h
#define RedBlackTree_h
 
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
 
 
typedef int ElementType;
 
typedef enum {
 RED,
 BLACK
} COLOR;
 
typedef struct RedBlackNode *RedBlackTree,*Position;
 
struct RedBlackNode{
 ElementType Element;
 COLOR Color;
 RedBlackTree Left;
 RedBlackTree Right;
};
 
static Position NullNode = NULL;
static Position Header;
static Position X,P,GP,GGP;
/* 初始化 */
RedBlackTree Initialize();
/* 插入 */
RedBlackTree Insert(RedBlackTree T,ElementType Item);
/* 刪除 */
RedBlackTree Remove(RedBlackTree T,ElementType Item);
/* 查找 */
Position Find(RedBlackTree T,ElementType Item);
/* 遍歷 */
void Travel(RedBlackTree T);
 
 
 
 
#endif /* RedBlackTree_h */

3.2 實現文件

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
//
// RedBlackTree.c
// RedBlackTree3
//
// Created by Wuyixin on 2017/7/3.
// Copyright © 2017年 Coding365. All rights reserved.
//
 
#include "RedBlackTree.h"
 
 
/* 左旋轉 */
static Position SingleRotateLeft(Position X);
/* 右旋轉 */
static Position SingleRotateRight(Position X);
/* 旋轉 */
static Position Rotate(Position Parent,Position* Origin ,ElementType Item);
 
 
/* 左旋轉 */
static Position SingleRotateLeft(Position T){
 Position TL = T->Left;
 T->Left = TL->Right;
 TL->Right = T;
 return TL;
}
/* 右旋轉 */
static Position SingleRotateRight(Position T){
 Position TR = T->Right;
 T->Right = TR->Left;
 TR->Left = T;
 return TR;
}
 
/* 旋轉 */
static Position Rotate(Position Parent,Position* Origin ,ElementType Item){
 if (Item < Parent->Element){
 if (Origin != NULL)
  *Origin = Parent->Left;
 return Parent->Left = Item < Parent->Left->Element ?
 SingleRotateLeft(Parent->Left) :
 SingleRotateRight(Parent->Left);
 }
 else{
 if (Origin != NULL)
  *Origin = Parent->Right;
 return Parent->Right = Item < Parent->Right->Element ?
 SingleRotateLeft(Parent->Right) :
 SingleRotateRight(Parent->Right);
 }
 
}
 
 
/* 初始化 */
RedBlackTree Initialize(){
 
 if (NullNode == NULL){
 NullNode = malloc(sizeof(struct RedBlackNode));
 if (NullNode == NULL)
  exit(EXIT_FAILURE);
 NullNode->Element = INT_MAX;
 NullNode->Color = BLACK;
 NullNode->Left = NullNode->Right = NullNode;
  
 }
 
 Header = malloc(sizeof(struct RedBlackNode));
 if (Header == NULL)
 exit(EXIT_FAILURE);
 
 /* header的值為無窮小，所以根插入到右邊*/
 Header->Element = INT_MIN;
 Header->Left = Header->Right = NullNode;
 Header->Color = BLACK;
 
 return Header;
 
}
 
static Position GetSibling(Position Parent,Position X){
 if (Parent->Element == INT_MIN)
 return NULL;
 if (X == Parent->Left)
 return Parent->Right;
 else if (X == Parent->Right)
 return Parent->Left;
 else
 return NULL;
}
 
void HandleReorientForInsert(ElementType Item){
 Position Sibling,Origin;
 
 /* 當P與X同時為紅節點才進行調整 */
 if (X == NullNode || !(P->Color == RED && X->Color == RED))
 return ;
 
 
 Sibling = GetSibling(GP, P);
 
 if (Sibling == NULL)
 return ;
 
 
 /* GP,P,X是成字型，調整為一字型 */
 if ((GP->Element < Item) != (P->Element < Item)){
 P = Rotate(GP, &Origin,Item);
 X = Origin;
 }
 
 GP = Rotate(GGP, &Origin,Item);
 P = Origin;
 
 /* P的兄弟是黑色的 */
 if (Sibling->Color == BLACK){
  
 GP->Color = BLACK;
 GP->Left->Color = RED;
 GP->Right->Color = RED;
  
 }
 /* P的兄弟是紅的 */
 else{
  
 GP->Color = RED;
 GP->Left->Color = BLACK;
 GP->Right->Color = BLACK;
 }
}
 
RedBlackTree _Insert(RedBlackTree T,ElementType Item){
 
 if (T == NullNode){
 T = malloc(sizeof(struct RedBlackNode));
 T->Element = Item;
 T->Left = T->Right = NullNode;
 T->Color = RED;
 }
 else if (Item < T->Element)
 T->Left = _Insert(T->Left, Item);
 else if (Item > T->Element)
 T->Right = _Insert(T->Right, Item);
 /* 重復值不插入 */
 
 X = P,P = GP,GP = GGP, GGP = T;
 
 HandleReorientForInsert(Item);
 
 return T;
}
 
/* 插入 */
RedBlackTree Insert(RedBlackTree T,ElementType Item){
 GGP = GP = P = X = NullNode;
 T = _Insert(T, Item);
 T->Right->Color = BLACK;
 return T;
}
 
 
static void _HandleReorientForRemove(ElementType Item){
 RedBlackTree Sibling,R;
 Sibling = GetSibling(P, X);
 
 if (Sibling == NULL)
 return ;
 
 if (Sibling->Left->Color == BLACK && Sibling->Right->Color == BLACK){
 P->Color = BLACK;
 X->Color = RED;
 Sibling->Color = RED;
 }else if(Sibling->Left->Color == RED){
 R = Sibling->Left;
  
 P->Color = BLACK;
 X->Color = RED;
  
 R = Rotate(P, NULL, R->Element);
 GP = Rotate(GP, NULL, R->Element);
  
 }else if (Sibling->Right->Color == RED){
 X->Color = RED;
 P->Color = BLACK;
 Sibling->Color = RED;
 Sibling->Right->Color = BLACK;
  
 GP = Rotate(GP, NULL, Sibling->Element);
  
 }
}
 
static void HandleReorientForRemove(RedBlackTree T, ElementType Item){
 RedBlackTree Sibling,Origin,OriginGP;
 if (X == NullNode)
 return ;
 
 /* X有兩個黑兒子 */
 if (X->Left->Color == BLACK && X->Right->Color == BLACK){
 _HandleReorientForRemove(Item);
 }else{
  
 OriginGP = GP;
 /* 落到下一層 */
 GP = P; P = X;
  
 if (Item < X->Element)
  X = X->Left;
 else
  X = X->Right;
  
  
 Sibling = GetSibling(P, X);
 /* 如果X是黑的，則Sibling是紅的，旋轉 */
 if (X->Color == BLACK){
  GP = Rotate(GP, &Origin, Sibling->Element);
  P = Origin;
  GP->Color = BLACK;
  P->Color = RED;
  _HandleReorientForRemove(Item);
  
 }
  
 /* 恢復X,PX,GP。由于X是當前節點 如果當前節點正是Item，不恢復會影響查找 */
 if (X->Element == Item){
  X = P ; P = GP ;GP = OriginGP;
 }
  
 }
}
 
/* 刪除 */
RedBlackTree Remove(RedBlackTree T,ElementType Item){
 
 ElementType Origin;
 Position DeletePtr;
 Origin = NullNode->Element;
 
 NullNode->Element = Item;
 
 GP = P = X = T;
 
 /* 根染紅 */
 T->Right->Color = RED;
 
 while (X->Element != Item) {
 GP = P ; P = X;
 if (Item < X->Element)
  X = X->Left;
 else
  X = X->Right;
  
 HandleReorientForRemove(T, Item);
 }
 
 
 NullNode->Element = Origin;
 
 /* 找到 */
 if (X != NullNode){
 DeletePtr = X; 
 if (X->Left != NullNode){
  GP = P ; P = X; X = X->Left;
  HandleReorientForRemove(T, Item);
  /* 尋找左子樹最大值替換 */
  while (X->Right != NullNode) {
  GP = P ; P = X;
  X = X->Right;
  HandleReorientForRemove(T, Item);
  }
  if (X == P->Left)
  P->Left = X->Left;
  else
  P->Right = X->Left;
  
 }else if (X->Right != NullNode){
  GP = P ; P = X; X = X->Right;
  HandleReorientForRemove(T, Item);
  /* 尋找右子樹最大值替換 */
  while (X->Left != NullNode) {
  GP = P ; P = X;
  X = X->Left;
  HandleReorientForRemove(T, Item);
  }
  if (X == P->Left)
  P->Left = X->Right;
  else
  P->Right = X->Right;
 }else{
  /* X是樹葉 */
  if (X == P->Left)
  P->Left = NullNode;
  else
  P->Right = NullNode;
 }
  
 DeletePtr->Element = X->Element;
 free(X);
  
 }
 
 /* 根染黑 */
 T->Right->Color = BLACK;
 
 return T;
}
 
 
 
typedef enum {
 ROOT,
 LEFT,
 RIGHT
} NodeType;
 
static char *TypeC;
static char *ColorC;
 
void _Travel(RedBlackTree T , NodeType Type){
 
 if (T != NullNode){
  
 if (Type == ROOT)
  TypeC = "root";
 else if (Type == LEFT)
  TypeC = "left";
 else if (Type == RIGHT)
  TypeC = "right";
  
 if (T->Color == BLACK)
  ColorC = "black";
 else
  ColorC = "red";
  
 printf("(%d,%s,%s) ",T->Element,ColorC,TypeC);
  
 _Travel(T->Left, LEFT);
 _Travel(T->Right, RIGHT);
  
 }
 
}
 
/* 遍歷 */
void Travel(RedBlackTree T){
 _Travel(T->Right,ROOT);
}

3.3 調用

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//
// main.c
// RedBlackTree3
//
// Created by Wuyixin on 2017/7/3.
// Copyright © 2017年 Coding365. All rights reserved.
//
 
#include "RedBlackTree.h"
int main(int argc, const char * argv[]) {
   
  RedBlackTree T = Initialize();
   
  T = Insert(T, 10);
  T = Insert(T, 85);
  T = Insert(T, 15);
  T = Insert(T, 70);
  T = Insert(T, 20);
  T = Insert(T, 60);
  T = Insert(T, 30);
  T = Insert(T, 50);
  T = Insert(T, 65);
  T = Insert(T, 80);
  T = Insert(T, 90);
  T = Insert(T, 40);
  T = Insert(T, 5);
  T = Insert(T, 55);
  T = Insert(T, 100);
   
   
  T = Remove(T, 100);
   
   
  Travel(T);
   
   
  return 0;
}

以上就是關于數據結構與算法中紅黑二叉樹的詳解，如有疑問請留言或者到本站的社區討論，感謝閱讀，希望能幫助到大家，謝謝大家對本站的支持！

原文鏈接：http://blog.csdn.net/xiaohusaier/article/details/75731526

延伸 · 閱讀

精彩推薦
  • C/C++C語言實現電腦關機程序

    C語言實現電腦關機程序

    這篇文章主要為大家詳細介紹了C語言實現電腦關機程序，文中示例代碼介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們可以參考一下...

    xiaocaidayong8482021-08-20
  • C/C++詳解c語言中的 strcpy和strncpy字符串函數使用

    詳解c語言中的 strcpy和strncpy字符串函數使用

    strcpy 和strcnpy函數是字符串復制函數。接下來通過本文給大家介紹c語言中的strcpy和strncpy字符串函數使用，感興趣的朋友跟隨小編要求看看吧...

    spring-go5642021-07-02
  • C/C++C++之重載 重定義與重寫用法詳解

    C++之重載 重定義與重寫用法詳解

    這篇文章主要介紹了C++之重載 重定義與重寫用法詳解,本篇文章通過簡要的案例,講解了該項技術的了解與使用,以下就是詳細內容,需要的朋友可以參考下...

    青山的青6062022-01-04
  • C/C++學習C++編程的必備軟件

    學習C++編程的必備軟件

    本文給大家分享的是作者在學習使用C++進行編程的時候所用到的一些常用的軟件，這里推薦給大家...

    謝恩銘10102021-05-08
  • C/C++深入理解goto語句的替代實現方式分析

    深入理解goto語句的替代實現方式分析

    本篇文章是對goto語句的替代實現方式進行了詳細的分析介紹，需要的朋友參考下...

    C語言教程網7342020-12-03
  • C/C++C語言中炫酷的文件操作實例詳解

    C語言中炫酷的文件操作實例詳解

    內存中的數據都是暫時的,當程序結束時,它們都將丟失,為了永久性的保存大量的數據,C語言提供了對文件的操作,這篇文章主要給大家介紹了關于C語言中文件...

    針眼_6702022-01-24
  • C/C++c++ 單線程實現同時監聽多個端口

    c++ 單線程實現同時監聽多個端口

    這篇文章主要介紹了c++ 單線程實現同時監聽多個端口的方法，幫助大家更好的理解和學習使用c++，感興趣的朋友可以了解下...

    源之緣11542021-10-27
  • C/C++C/C++經典實例之模擬計算器示例代碼

    C/C++經典實例之模擬計算器示例代碼

    最近在看到的一個需求，本以為比較簡單，但花了不少時間，所以下面這篇文章主要給大家介紹了關于C/C++經典實例之模擬計算器的相關資料，文中通過示...

    jia150610152021-06-07
主站蜘蛛池模板： 久久综合亚洲 | 久久精品 | 国产精品久久久久久婷婷天堂 | 日韩一区二区三区在线观看 | 国产亚洲一区二区精品 | 日韩电影中文字幕 | 亚洲国产精品99久久久久久久久 | 免费三级黄色 | 欧美成人视屏 | 国产精品九九九 | 91亚洲国产 | 成人免费视频网址 | 欧美日韩在线免费 | av电影免费在线 | 亚洲国产精品免费在线观看 | 中文字幕一区二区在线观看 | 免费观看a视频 | 亚洲精品一区二区在线观看 | 亚洲免费观看视频 | 亚洲一区二区精品 | 在线播放黄 | 91久久国产露脸精品国产护士 | 亚洲一区二区三区精品动漫 | 精品午夜久久 | 欧美日韩精品免费 | 日韩欧美精品一区二区三区 | 久久九 | 国产精品一级大片 | 超黄毛片 | 日韩精品一区二区在线观看 | 日韩国产在线观看 | 69免费视频| 免费的av网站 | 天天操人人干 | 欧美日韩免费一区二区三区 | 免费污污视频在线观看 | 午夜免费视频网站 | 亚洲专区中文字幕 | 免播放器看av | 久久中文字幕一区二区 | 欧美日本精品 |