??博客代碼已上傳至gitee:https://gitee.com/byte-binxin/cpp-class-code
概念
二叉搜索樹雖可以縮短查找的效率,但如果數(shù)據(jù)有序或接近有序二叉搜索樹將退化為單支樹,查找元素相當于在順序表中搜索元素,效率低下。因此,兩位俄羅斯的數(shù)學家G.M.Adelson-Velskii和E.M.Landis在1962年發(fā)明了一種解決上述問題的方法:當向二叉搜索樹中插入新結點后,如果能保證每個結點的左右子樹高度之差的絕對值不超過1(需要對樹中的結點進行調整),即可降低樹的高度,從而減少平均搜索長度。
- 它的左右子樹都是AVL樹
- 左右子樹高度之差的絕對值(也叫平衡因子)不超過1
- 我規(guī)定:平衡因子(balance factor)= 右子樹高度 - 左子樹高度(后面這樣實現(xiàn))
AVL樹的實現(xiàn)
AVL樹的節(jié)點定義
這里節(jié)點是一個三叉鏈,里面存放了元素的數(shù)據(jù)和該節(jié)點此時的平衡因子。不管今后我們進行什么操作,都要維持這里的平衡因子的絕對值不超過1。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
template<class K, class V>struct AVLTreeNode{ // 三叉鏈 AVLTreeNode<K, V>* _left; AVLTreeNode<K, V>* _right; AVLTreeNode<K, V>* _parent; pair<K, V> _kv; int _bf; // balance factor 平衡因子 右子樹高度-左子樹高度 AVLTreeNode(const pair<K, V>& kv) :_left(nullptr) ,_right(nullptr) ,_parent(nullptr) ,_kv(kv) ,_bf(0) {}}; |
AVL樹的插入
方法概述
第一步: 我們先按照二叉搜索樹樹插入節(jié)點的方式,插入節(jié)點(這一步很簡單,上一篇博客介紹過)
第二步: 更新平衡因子,更新平衡因子的過程是一個難點,下面我給大家分析一下整個過程
平衡因子的調節(jié)
正常情況
實際上,我們應該能夠發(fā)現(xiàn),插入一個節(jié)點后,它之后影響它祖先的平衡因子(可能是所有祖先,也可能是一部分祖先),下面就是一個分析過程:
第一步: 判斷父親節(jié)點是否存在,不存在直接結束,如果存在,且插入節(jié)點是它的左孩子,那么父親節(jié)點的平衡因子就減1,如果是父親的右,父親的平衡因子就加1。然后對父親節(jié)點的平衡因子進行檢索。
第二步: 繼續(xù)對父親節(jié)點的平衡因子進行檢索,平衡因子會有一下三種情況
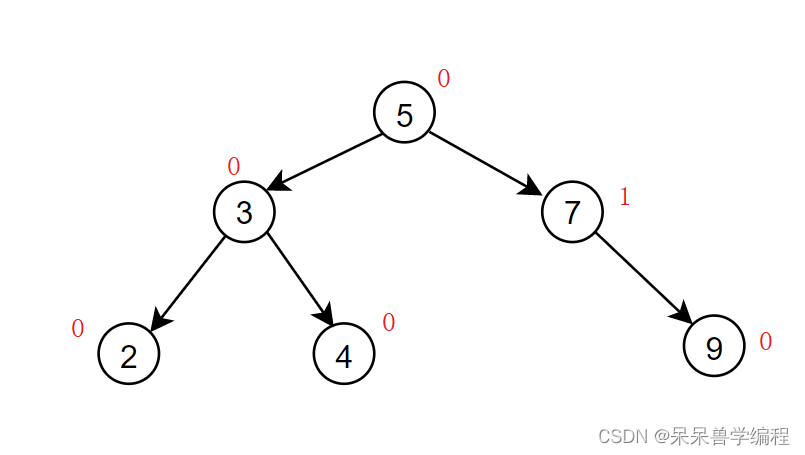
第一種情況: 此時父親的平衡因子為0,則說明插入前父親的平衡因子為1或-1,缺少左節(jié)點或右節(jié)點插入后,插入的節(jié)點已經補齊了左節(jié)點或右節(jié)點,整體高度不變,對上層無影響,不需要繼續(xù)調節(jié)。下面是一個演示圖:
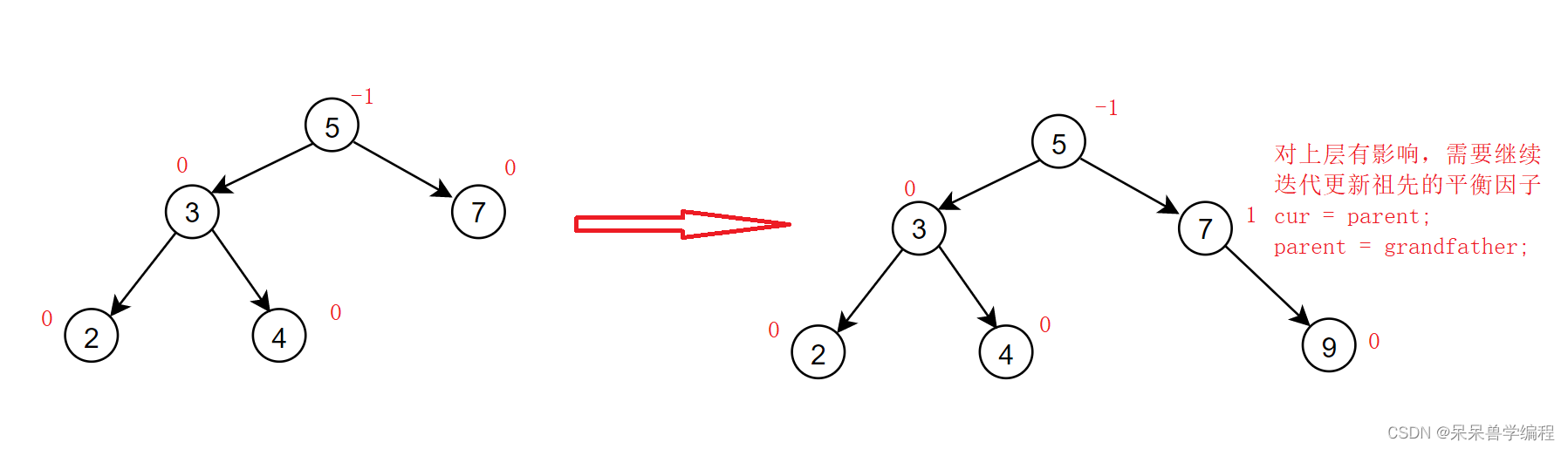
第二種情況 此時父親節(jié)點的平衡因子為-1或1,則說明插入前父親的平衡因子為0,插入后增加了一個左節(jié)點或右節(jié)點,整體高度增加1,對上層有影響,繼續(xù)迭代更新祖先的平衡因子。下面是一個演示圖:
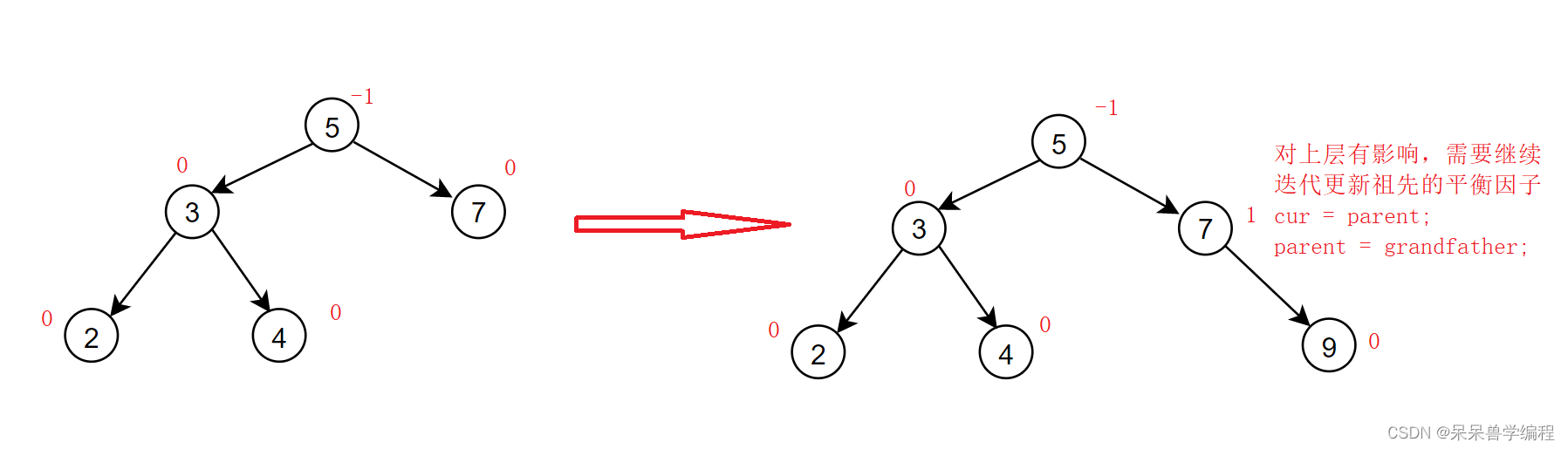
第三種情況: 此時父親節(jié)點的平衡因子為-2或2,則說明插入前父親的平衡因子為-1或1,多了一個左節(jié)點或一個右節(jié)點,插入后增加了一個左節(jié)點或右節(jié)點,此時多了兩個左節(jié)點和右節(jié)點,這棵子樹一邊已經被拉高了,此時這棵子樹不平衡了,需要旋轉處理。下面是一個演示圖:

旋轉處理(出現(xiàn)了不平衡子樹)
旋轉有四種情況:
1.左單旋(新插入的節(jié)點在右子樹的右側)
具體步驟: 讓subR的左孩子成為parent的右孩子,然后讓parent成為subR的左孩子,最后把兩個節(jié)點的平衡因子修改為0.
先畫一個具像圖給大家演示如何進行這個操作(下面是一部分失衡的子樹):

再畫一個抽像圖來演示:

代碼實現(xiàn)如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
// 左單旋 bf為2 右邊高,把上面的壓下來放到左邊void RotateL(Node* parent){ Node* subR = parent->_right; Node* subRL = subR->_left; // 1.先讓把subR的左邊(可能為空也可能不為空)作為parent的右邊 parent->_right = subRL; // 2.如果subRL不為空,就讓subRL的父指針指向parent if (subRL) subRL->_parent = parent; // 3.先記錄parent的父節(jié)點的位置,然后把parent作為subR的左邊 Node* ppNode = parent->_parent; subR->_left = parent; // 4.parent的父指針指向subR parent->_parent = subR; // 5.如果ppNode為空==>說明subR現(xiàn)在是根節(jié)點,就讓subR的父指針指向nullptr // 不是根節(jié)點就把subR的父指針指向parent的父節(jié)點,parent的父節(jié)點(左或右)指向subR if (ppNode == nullptr) { // 更新根節(jié)點 _root = subR; subR->_parent = nullptr; } else { // 判斷parent是ppNode的左還是右 if (ppNode->_left == parent) ppNode->_left = subR; else ppNode->_right = subR; subR->_parent = ppNode; } // 6.把parent和subR的平衡因子更新為0 subR->_bf = parent->_bf = 0;} |
2.右單旋 (新節(jié)點插入到較高左子樹的左側)
具體步驟: 讓subL的右孩子成為parent的左孩子,然后讓parent成為subL的右孩子,最后把兩個節(jié)點的平衡因子修改為0.
先畫一個具像圖給大家演示如何進行這個操作(下面是一部分失衡的子樹):

在給大家演示一下抽象圖:

代碼實現(xiàn)如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
// 右單旋 bf為-2 左邊高,把上面的壓下來放到右邊void RotateR(Node* parent){ Node* subL = parent->_left; Node* subLR = subL->_right; // 1.先讓把subL的右邊(可能為空也可能不為空)作為parent的左邊 parent->_left = subLR; // 2.如果subLR不為空,就讓subLR的父指針指向parent if (subLR) subLR->_parent = parent; // 3.先記錄parent的父節(jié)點的位置,然后把parent作為subL的右邊 Node* ppNode = parent->_parent; subL->_right = parent; // 4.parent的父指針指向subL parent->_parent = subL; // 5.如果ppNode為空==>說明subR現(xiàn)在是根節(jié)點,就讓subL的父指針指向nullptr // 不是根節(jié)點就把subL的父指針指向parent的父節(jié)點,parent的父節(jié)點(左或右)指向subL if (ppNode == nullptr) { // 更新根節(jié)點 _root = subL; subL->_parent = nullptr; } else { // 判斷parent是ppNode的左還是右 if (ppNode->_left == parent) ppNode->_left = subL; else ppNode->_right = subL; subL->_parent = ppNode; } // 6.把parent和subL的平衡因子更新為0 subL->_bf = parent->_bf = 0;} |
3.右左雙旋(新節(jié)點插入在較高右子樹左側,這里和第一種情況的區(qū)別就是前者是直線,后者是折線)
具體步驟 先對subR進行一個右單旋,然后對parent進行左單旋,修改平衡因子,有三種改法。
三個節(jié)點從左至右的三個節(jié)點一次是:parent、subRL和subR。
如果subRL的平衡因子為0,就將它們依次改為0,0, 0;
如果subRL的平衡因子為1,就將它們依次改為-1,0, 0;
如果subRL的平衡因子為-1,就將它們依次改為0,0, 1。
先看具像圖:

再看一個抽象圖(兩種情況):
subRL的bf為1

subRL的bf為-1

代碼實現(xiàn)如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// 右左旋轉==>parent->_bf==2&&cur->_bf==-1void RotateRL(Node* parent){ Node* subR = parent->_right; Node* subRL = subR->_left; int bf = subRL->_bf;// 保留subRL的平衡因子的值,方便知道新插入的節(jié)點是在subRL的左子樹還是右子樹 // 旋轉 先對subR進行右旋轉,再對parent進行左旋轉 RotateR(subR); RotateL(parent); // 從左到右 parent subRL subR if (bf == -1)// subRL的左子樹 bf: 0 0 1 { parent->_bf = 0; subRL->_bf = 0; subR->_bf = 1; } else if (bf == 1)// subRL的右子樹 bf: -1 0 0 { parent->_bf = -1; subRL->_bf = 0; subR->_bf = 0; } else if (bf == 0) { parent->_bf = 0; subRL->_bf = 0; subR->_bf = 0; }} |
4.左右雙旋(新節(jié)點插入在較高右子樹左側,這里和第一種情況的區(qū)別就是前者是直線,后者是折線)
具體步驟先對subL進行一個左單旋,然后對parent進行右單旋,修改平衡因子,有三種改法。三個節(jié)點從左至右的三個節(jié)點一次是:subL、subLR和parent。(和上面的類似,這樣有助于我們記住平衡因子的調整,同時我們也可以畫簡圖理解記憶)
如果subLR的平衡因子為0,就將它們依次改為0,0, 0;
如果subLR的平衡因子為1,就將它們依次改為-1,0, 0;
如果subLR的平衡因子為-1,就將它們依次改為0,0, 1。
先看具像圖:

再看一個抽象圖(也有兩種情況):
subLR的bf為-1

subLR的bf為1

代碼實現(xiàn)如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// 左右旋轉==>parent->_bf==-2&&cur->_bf==1void RotateLR(Node* parent){ Node* subL = parent->_left; Node* subLR = subL->_right; int bf = subLR->_bf;// 保留subLR的平衡因子的值,方便知道新插入的節(jié)點是在subLR的左子樹還是右子樹 // 旋轉 先對subL進行左旋轉,再對parent進行右旋轉 RotateL(subL); RotateR(parent); // 從左到右 subL subLR parent if (bf == -1)// subLR的左子樹 bf: 0 0 1 { subL->_bf = 0; subLR->_bf = 0; parent->_bf = 1; } else if (bf == 1)// subLR的右子樹 bf: -1 0 0 { subL->_bf = -1; subLR->_bf = 0; parent->_bf = 0; } else if (bf == 0) { subL->_bf = 0; subLR->_bf = 0; parent->_bf = 0; }} |
插入代碼實現(xiàn)
插入的步驟也就是如上面說的一樣,下面的代碼我們通過迭代實現(xiàn)。
代碼實現(xiàn)如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
|
bool Insert(const pair<K, V>& kv){ // 先按照二叉搜索數(shù)一樣插入元素 // 無節(jié)點是插入 if (_root == nullptr) { _root = new Node(kv); return true; } // 有節(jié)點時插入 Node* parent = nullptr; Node* cur = _root; while (cur) { parent = cur; // 小于往左走 if (kv.first < cur->_kv.first) { cur = cur->_left; } // 大于往右走 else if (kv.first > cur->_kv.first) { cur = cur->_right; } else { // 找到了,就返回false return false; } } cur = new Node(kv); // 判斷cur應該插在parent的左還是右 // 小于在左,大于在右 if (cur->_kv.first < parent->_kv.first) { parent->_left = cur; cur->_parent = parent; } else { parent->_right = cur; cur->_parent = parent; } // 更新parent的平衡因子 // 節(jié)點的插入只會影響cur的祖先的平衡因子(不是所有的,是一部分,分情況) while (parent) { // 更新parent的平衡因子 // cur在parent的左,parent->_bf-- // cur在parent的右,parent->_bf++ if (cur == parent->_left) parent->_bf--; else parent->_bf++; // bf 可能為 -2、-1、0、1、2 // 如果平衡因子為0,說明更新之前,parent的bf為-1或1,現(xiàn)在補齊了左節(jié)點或右節(jié)點,bf==0,對上層無影響 // 如果平衡因子為-1或1,說明更新之前,parent的bf為0,現(xiàn)在增加了一個左節(jié)點或有節(jié)點,bf==-1 || bf==1,對上層有影響 // 如果平衡因子為-2或2,說明更新之前,parent的bf為-1或1,現(xiàn)在往左(右)節(jié)點補了左(右)節(jié)點,也就是一邊 // 拉高了,樹不平衡了,需要用左旋轉或右旋轉來進行調整 if (parent->_bf == 0) { // 對上層無影響,退出 break; } else if (parent->_bf == -1 || parent->_bf == 1) { // 對上層有影響,迭代更新 cur = parent; parent = parent->_parent; } else { // 平衡樹出現(xiàn)了問題,需要調整 // 1.右邊高,左旋轉調整 if (parent->_bf == 2) { // 如果是一條直線==>左旋轉即可 // 如果是一條折線==>右左旋轉 if (cur->_bf == 1) RotateL(parent); else if (cur->_bf == -1) RotateRL(parent); } // 2.左邊高,右旋轉調整 else if (parent->_bf == -2) { // 如果是一條直線==>右旋轉即可 // 如果是一條折線==>左右旋轉 if (cur->_bf == -1) RotateR(parent); else if (cur->_bf == 1) RotateLR(parent); } // 調整后是平衡樹,bf為0,不需要調整了 break; } } return bool;} |
AVL樹的查找
查找的代碼和二叉搜索樹是一樣的,這里就不過多介紹。
代碼實現(xiàn)如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
bool Find(const K& key){ if (_root == nullptr) return false; Node* cur = _root; while (cur) { // 小于往左走 if (key < cur->_kv.first) { cur = cur->_left; } // 大于往右走 else if (key > cur->_kv.first) { cur = cur->_right; } else { // 找到了 return true; } } return false;} |
AVL樹的刪除
方法概述
第一步: 我們先按照二叉搜索樹樹刪除節(jié)點的方式,刪除節(jié)點(這一步很簡單,上一篇博客介紹過)
第二步: 然后根據(jù)對應刪除情況更新平衡因子,這里更新平衡因子的方法與插入的更新方法是相反的,下面我給大家分析一下整個過程
平衡因子的調節(jié)
正常情況
刪除節(jié)點后,如果刪除的節(jié)點為根節(jié)點,就結束。否則根據(jù)刪除節(jié)點為父節(jié)點的左右調整父節(jié)點的平衡因子。如果刪除節(jié)點是父節(jié)點的左孩子,那么父親節(jié)點的平衡因子加1,否則減1。然后對父親節(jié)點進行檢索。
有以下幾種情況:
第一種情況: 此時父親的平衡因子為0,則說明刪除前父親的平衡因子為1或-1,多出一個左節(jié)點或右節(jié)點,刪除節(jié)點后,左右高度相等,整體高度減1,對上層有影響,需要繼續(xù)調節(jié)。下面是一個演示圖:(如果此時3為根節(jié)點,那么也可以結束)

第二種情況: 此時父親的平衡因子為-1或1,則說明刪除前父親的平衡因子為0,左右高度相等,刪除節(jié)點后,少了一個左節(jié)點或右節(jié)點,但是整體高度不變,對上層無影響,不需要繼續(xù)調節(jié)。下面是一個演示圖:

第三種情況: 此時父親節(jié)點的平衡因子為-2或2,則說明刪除前父親的平衡因子為-1或1,多了一個左節(jié)點或一個右節(jié)點,刪除了一個右節(jié)點或左節(jié)點,此時多了兩個左節(jié)點和右節(jié)點,這棵子樹一邊已經被拉高了,此時這棵子樹不平衡了,需要旋轉處理。下面是一個演示圖:

需要旋轉處理的幾種情況
這里我只分析右邊高的情況,左邊高和它對稱的,操作是相同的。
情況一:
操作方法: 對parent進行左旋轉,因為subR的平衡因子為0,需要繼續(xù)檢索,然后繼續(xù)迭代,把cur迭代sub的位置,parent到cur的父親的位置
具像圖:

抽象圖:

情況二:
操作方法: 對parent進行左旋,然后修改平衡因子,把subR的平衡因子改為-1,parent的平衡因子改為1,因為subR的平衡因子為-1,所以無需迭代,直接結束
具像圖:

抽象圖:

情況三:
操作方法: 對subR進行右旋,然后對parent進行左旋,此時subR的平衡因子為0,需迭代
具像圖:
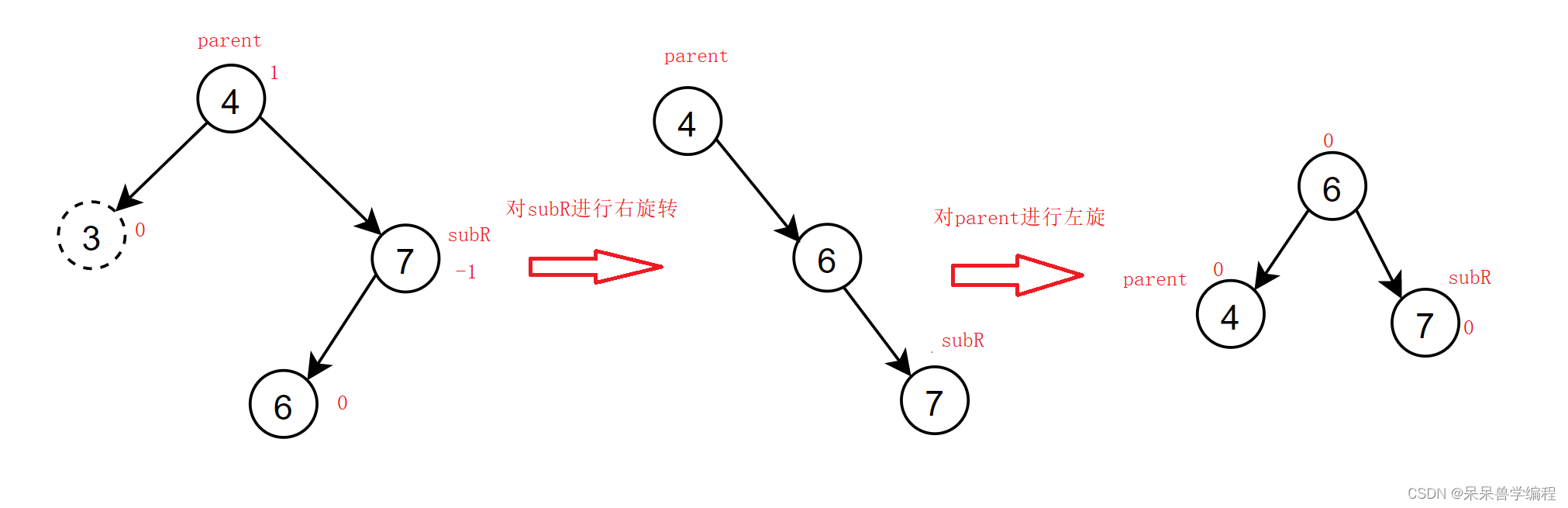
抽象圖:

刪除代碼如下
刪除代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
|
bool Erase(const K& key){ if (_root == nullptr) return false; // 有節(jié)點時插入 Node* parent = nullptr; Node* cur = _root; while (cur) { // 小于往左走 if (key < cur->_kv.first) { parent = cur; cur = cur->_left; } // 大于往右走 else if (key > cur->_kv.first) { parent = cur; cur = cur->_right; } else { // 找到了 // 1.左邊為空,把parent指向cur的右 // 2.右邊為空,把parent指向cur的左 // 3.左右都不為空,用右子樹的最左邊的節(jié)點(最小節(jié)點)的值替換要刪除的節(jié)點,然后轉換為用1的情況刪除該節(jié)點 if (cur->_left == nullptr) { if (cur == _root) { _root = cur->_right; delete cur; break; } else { if (parent->_left == cur) { parent->_left = cur->_right; parent->_bf++; } else { parent->_right = cur->_right; parent->_bf--; } } if (parent->_bf != -1 && parent->_bf != 1) AfterEraseUpdateBf(parent); delete cur; } else if (cur->_right == nullptr) { if (cur == _root) { _root = cur->_left; delete cur; break; } else { if (parent->_left == cur) { parent->_left = cur->_left; parent->_bf++; } else { parent->_right = cur->_left; parent->_bf--; } } if (parent->_bf != -1 && parent->_bf != 1) AfterEraseUpdateBf(parent); delete cur; } else { Node* rightMinParent = cur; Node* rightMin = cur->_right;// 先去右子樹 while (rightMin->_left) { rightMinParent = rightMin; rightMin = rightMin->_left;// 一種往左走 } cur->_kv = rightMin->_kv; // 替代刪除 // 刪除minNode 第一種情況:左節(jié)點為空 if (rightMinParent->_left == rightMin) { rightMinParent->_left = rightMin->_right; rightMinParent->_bf++; } else { rightMinParent->_right = rightMin->_right; rightMinParent->_bf--; } if (rightMinParent->_bf != -1 && rightMinParent->_bf != 1) AfterEraseUpdateBf(rightMinParent); delete rightMin; } return true; } } return false;}void AfterEraseUpdateBf(Node* parent){ if (parent == nullptr) return; Node* cur = parent; goto first; while (parent) { // 更新parent的平衡因子 // cur在parent的左,parent->_bf++ // cur在parent的右,parent->_bf-- if (cur == parent->_left) parent->_bf++; else parent->_bf--; // bf 可能為 -2、-1、0、1、2 // 如果平衡因子為0,說明更新之前,parent的bf為-1或1,現(xiàn)在刪掉了左節(jié)點或右節(jié)點,整體高度變了,對上層有影響 // 如果平衡因子為-1或1,說明更新之前,parent的bf為0,現(xiàn)在刪掉了一個左節(jié)點或有節(jié)點,整體高度不變,對上層無影響 // 如果平衡因子為-2或2,說明更新之前,parent的bf為-1或1,現(xiàn)在往左(右)節(jié)點補了左(右)節(jié)點,也就另一邊 // 拉高了,樹不平衡了,需要用左旋轉或右旋轉來進行調整 first: if (parent->_bf == 0) { // 對上層有影響,迭代更新 // 如果parent是根節(jié)點就結束 if (parent->_parent == nullptr) break; cur = parent; parent = parent->_parent; } else if (parent->_bf == -1 || parent->_bf == 1) { // 對上層無影響,退出 break; } else { // 平衡樹出現(xiàn)了問題,需要調整 // 1.右邊高,左旋轉調整 if (parent->_bf == 2) { // 如果是一條直線==>左旋轉即可 // 如果是一條折線==>右左旋轉 if (parent->_right->_bf == 1) { RotateL(parent); cur = parent->_parent; parent = cur->_parent; continue; } else if (parent->_right->_bf == -1)// 調整后 p sL s 如果sL是1或-1可以退出 { Node* s = parent->_right; Node* sL = s->_left; RotateRL(parent); // 不平衡向上調整 注意:bug1(以為調整完就是1或-1了,其實這里不是,畫圖思考一下) //if (sL->_bf != 1 && sL->_bf != -1) { cur = sL; parent = cur->_parent; continue; } } else if (parent->_right->_bf == 0)// 旋轉后平衡因子要修改,畫圖感受 parent: 1 parent->_parent:- 1 { RotateL(parent); parent->_bf = 1; parent->_parent->_bf = -1; } } // 2.左邊高,右旋轉調整 else if (parent->_bf == -2) { // 如果是一條直線==>右旋轉即可 // 如果是一條折線==>左右旋轉 if (parent->_left->_bf == -1) { RotateR(parent); cur = parent->_parent;// bug2 cur要變成這個位置是因為選擇后父親的位置變了,畫圖 parent = cur->_parent; continue;//parent不是-1或1就繼續(xù) } else if (parent->_left->_bf == 1)// 調整后 s sR p 如果sL是1或-1可以退出 { Node* s = parent->_left; Node* sR = s->_right; RotateLR(parent); // 不平衡向上調整 為0時如果parent為根 //if (sR->_bf != 1 && sR->_bf != -1) { cur = sR; parent = cur->_parent; continue; } } else if (parent->_left->_bf == 0)// 平衡因子要修改,畫圖感受 parent->_parent: 1 parent: -1 { RotateR(parent); parent->_parent->_bf = 1; parent->_bf = -1; } } // 調整后是平衡樹,bf為1或-1,不需要調整了 break; } }} |
AVL樹的測試代碼
下面是驗證是否為AVL樹的代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
int _Height(Node* root){ if (root == nullptr) return 0; int leftHeight = _Height(root->_left); int rightHeight = _Height(root->_right); return 1 + max(leftHeight, rightHeight);}bool _IsBalanceTree(Node* root){ if (root == nullptr) return true; int leftHeight = _Height(root->_left); int rightHeight = _Height(root->_right); return rightHeight - leftHeight == root->_bf && abs(rightHeight - leftHeight) < 2 && _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);} |
實例演示:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
void TestAVLTree1(){ AVLTree<int, int> at; srand((size_t)time(nullptr)); // int a[] = { 4,3,5,3,1,2,7 }; // int a[] = { 1,2,3,4,5,6,7,8,9 }; // int a[] = { 2,4,6,3,5,1,9,10,8,7 }; // int a[] = { 4,2,3,5 }; // int a[] = { 16,3,7,11,9,26,18,14,15 }; // int a[] = { 4,2,6,1,3,5,15,7,16,14 }; // int* a = new int[10000]; /*int i = 1; for (auto& e : a) { e = i++; }*/ vector<int> a; for (size_t i = 0; i < 13; ++i) { // a.push_back(rand()); a.push_back(13); } for (auto e : a) { int begin = clock(); pair<AVLTreeNode<int, int>*, bool> ret = at.Insert(make_pair(e, e)); int end = clock(); // cout << ret.first->_kv.second << endl; // cout << ret.first->_kv.second << ":" << ret.second << endl; cout << "插入 " << e << " 后變化 --> Height: " << at.Height() << " 是否為AVLTree:" << at.IsBalanceTree(); cout << " 用時: " << end - begin << "ms" << endl; } cout << "------------------------------------------------------" << endl; // at.InOrder(); for (auto e : a) { if (e == 11478) { int a = 0; } int begin = clock(); at.Erase(e); int end = clock(); cout << "刪除 " << e << " 后變化 --> Height: " << at.Height() << " 是否為AVLTree:" << at.IsBalanceTree(); cout << " 用時: " << end - begin << "ms" << endl; } at.InOrder();} |
代碼運行結果如下:

總結
AVL樹的全部內容就介紹到這,圖畫了一下午,創(chuàng)造不易,感謝支持,下一篇博客更新紅黑樹的相關內容,喜歡的話,歡迎點贊支持~

到此這篇關于C++數(shù)據(jù)結構AVL樹全面分析的文章就介紹到這了,更多相關C++ AVL樹內容請搜索服務器之家以前的文章或繼續(xù)瀏覽下面的相關文章希望大家以后多多支持服務器之家!
原文鏈接:https://blog.csdn.net/weixin_58450087/article/details/123090533