一、紅黑樹的概念

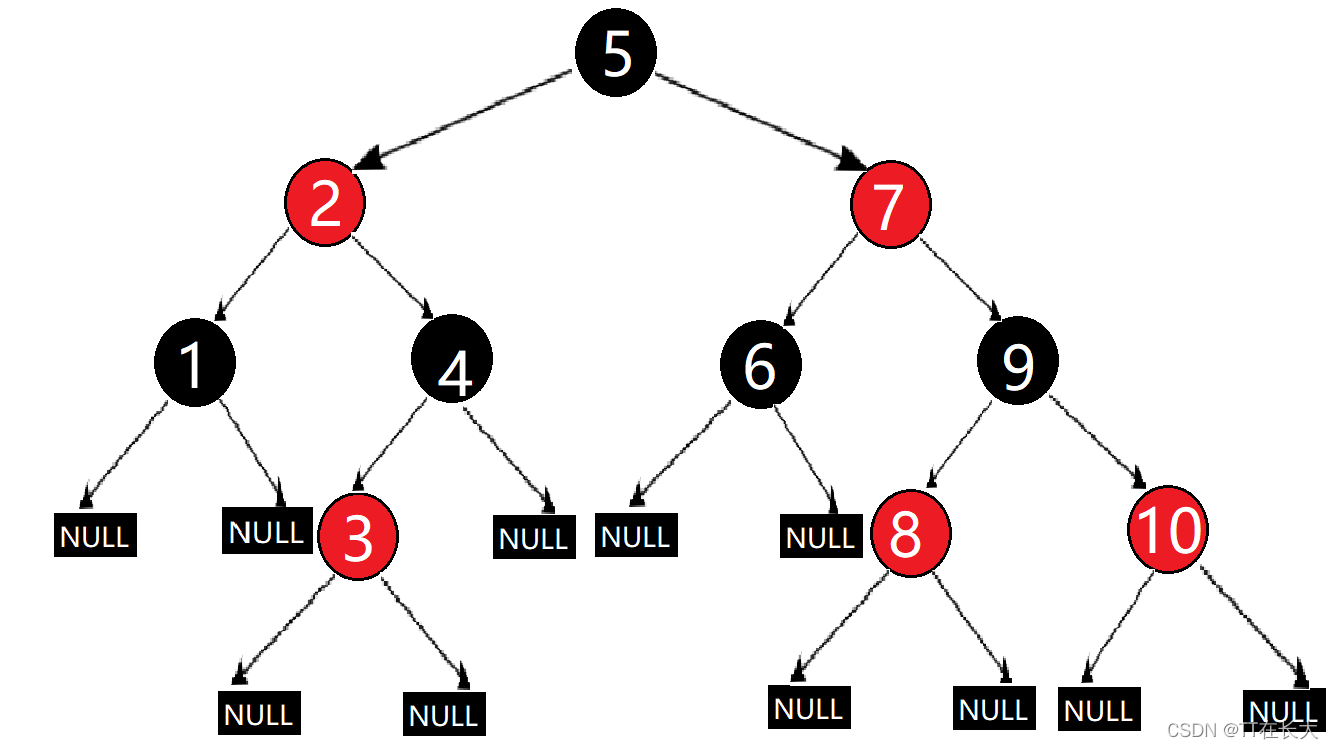
紅黑樹（Red Black Tree），是在計算機(jī)科學(xué)中用到的一種數(shù)據(jù)結(jié)構(gòu)，是一種二叉搜索樹，但在每個結(jié)點(diǎn)上增加一個存儲位表示結(jié)點(diǎn)的顏色，可以是Red或Black。 通過對任何一條從根到葉子的路徑上各個結(jié)點(diǎn)著色方式的限制，紅黑樹確保沒有一條路徑會比其他路徑長出倆倍，因而是接近平衡的。

二、紅黑樹的性質(zhì)

1. 每個結(jié)點(diǎn)不是紅色就是黑色；

2. 根節(jié)點(diǎn)是黑色的；

3. 如果一個節(jié)點(diǎn)是紅色的，則它的兩個孩子結(jié)點(diǎn)是黑色的；

4. 對于每個結(jié)點(diǎn)，從該結(jié)點(diǎn)到其所有后代葉結(jié)點(diǎn)的簡單路徑上，均 包含相同數(shù)目的黑色結(jié)點(diǎn)；

5. 每個葉子結(jié)點(diǎn)都是黑色的(此處的葉子結(jié)點(diǎn)指的是空結(jié)點(diǎn))；

滿足上面的性質(zhì)，紅黑樹就能保證其最長路徑中節(jié)點(diǎn)個數(shù)不會超過最短路徑節(jié)點(diǎn)個數(shù)的兩倍。

三、紅黑樹節(jié)點(diǎn)的定義

enum Colour		//紅黑樹顏色枚舉
{
	RED,
	BLACK,
};

template<class K, class V>
struct RBTreeNode					//節(jié)點(diǎn)結(jié)構(gòu)體
{
	RBTreeNode<K, V>* _left;		//左子樹
	RBTreeNode<K, V>* _right;		//右子樹
	RBTreeNode<K, V>* _parent;		//父節(jié)點(diǎn)

	pair<K, V> _kv;

	Colour _col;

	RBTreeNode(const pair<K, V>& kv)	//構(gòu)造函數(shù)
		: _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)
	{}
};

插入時默認(rèn)為紅色節(jié)點(diǎn)，因?yàn)榧t色可能會破壞規(guī)則3，黑色一定會破壞規(guī)則4，所以默認(rèn)紅色。

四、紅黑樹結(jié)構(gòu) 

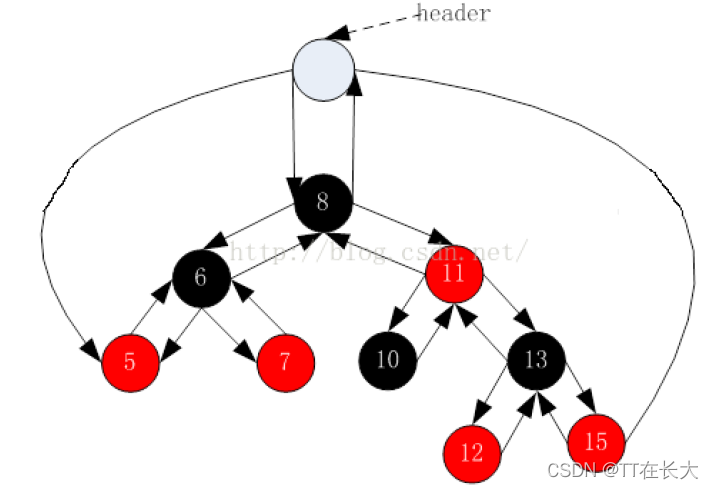
為了后續(xù)實(shí)現(xiàn)關(guān)聯(lián)式容器簡單，紅黑樹的實(shí)現(xiàn)中增加一個頭結(jié)點(diǎn)，因?yàn)楦?jié)點(diǎn)必須為黑色，為了與根節(jié)點(diǎn)進(jìn)行區(qū)分，將頭結(jié)點(diǎn)給成黑色，并且讓頭結(jié)點(diǎn)的 parent 域指向紅黑樹的根節(jié)點(diǎn)，left域指向紅黑樹中最小的節(jié)點(diǎn)，right域指向紅黑樹中最大的節(jié)點(diǎn)，如下:

五、 紅黑樹的插入操作

紅黑樹是在二叉搜索樹的基礎(chǔ)上加上其平衡限制條件，因此紅黑樹的插入可分為兩步：

1. 按照二叉搜索的樹規(guī)則插入新節(jié)點(diǎn)：

	pair<Node*, bool> Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return make_pair(_root, true);
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return make_pair(cur, false);
			}
		}

		Node* newNode = new Node(kv);
		newNode->_col = RED;
		if (parent->_kv.first > kv.first)
		{
			parent->_left = newNode;
			newNode->_parent = parent;
		}
		else
		{
			parent->_right = newNode;
			newNode->_parent = parent;
		}
		cur = newNode;

		while (parent && parent->_col == RED)		//違反規(guī)則三
		{

		}

		_root->_col = BLACK;		//插入結(jié)束再次將根變?yōu)楹?

		return make_pair(cur, true);
	}

2. 檢測新節(jié)點(diǎn)插入后，紅黑樹的性質(zhì)是否造到破壞

因?yàn)樾鹿?jié)點(diǎn)的默認(rèn)顏色是紅色，因此：如果其雙親節(jié)點(diǎn)的顏色是黑色，沒有違反紅黑樹任何性質(zhì)，則不需要調(diào)整；但當(dāng)新插入節(jié)點(diǎn)的雙親節(jié)點(diǎn)顏色為紅色時，就違反了性質(zhì)三不能有連在一起的紅色節(jié)點(diǎn)，此時需要對紅黑樹分情況來討論：

cur為當(dāng)前節(jié)點(diǎn)，p為父節(jié)點(diǎn)，g為祖父節(jié)點(diǎn)，u為叔叔節(jié)點(diǎn)

情況一：cur為紅，p為紅，g為黑，u存在且為紅

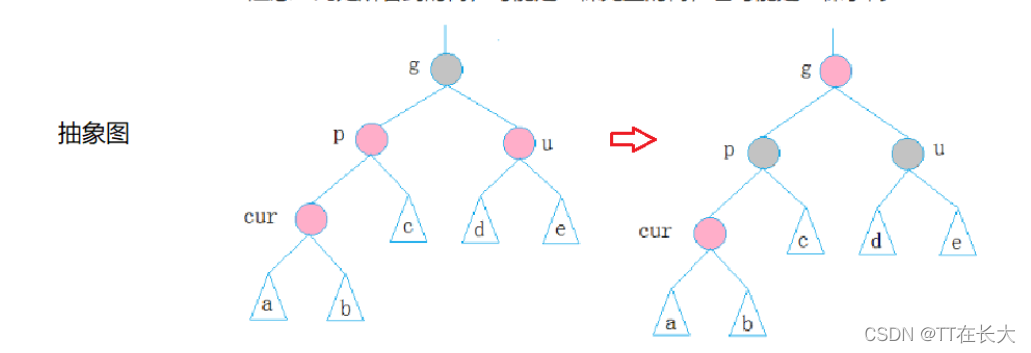
如果g是根節(jié)點(diǎn)，調(diào)整完成后，需要將g改為黑色，如果g是子樹，g一定有父節(jié)點(diǎn)，且如果為紅色呃，繼續(xù)向上調(diào)整。

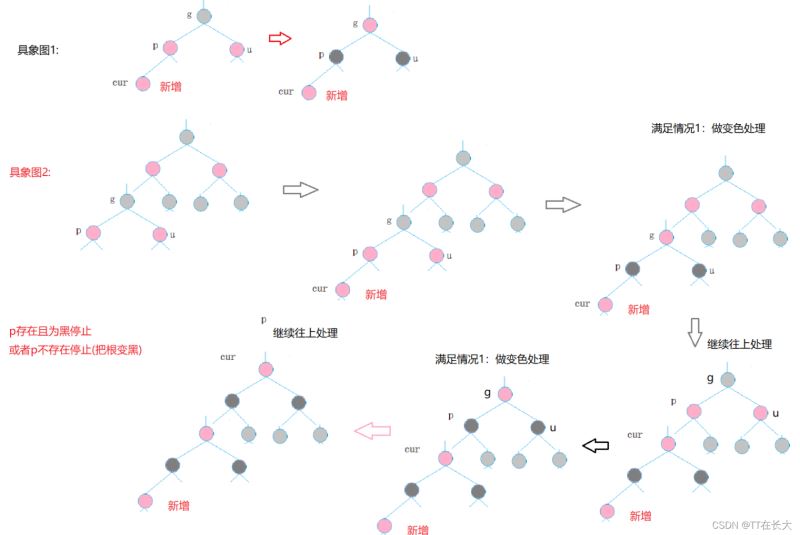
將p,u改為黑，g改為紅，然后把g當(dāng)成cur，繼續(xù)向上調(diào)整 。

情況二: cur為紅，p為紅，g為黑，u不存在/u為黑

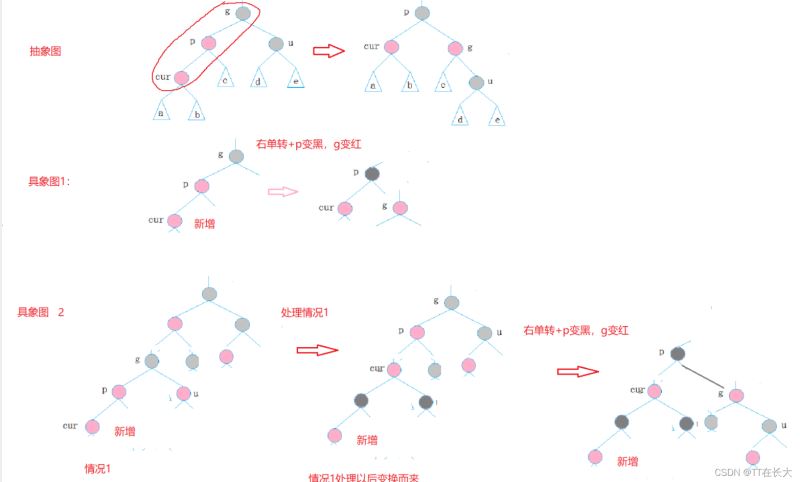
u的情況有兩種：

1.如果u節(jié)點(diǎn)不存在，則cur一定是新插入節(jié)點(diǎn)，因?yàn)槿绻鹀ur不是新插入節(jié)點(diǎn)，則cur和p一定有一個節(jié)點(diǎn)的顏色是黑色，就不滿足性質(zhì)4：每條路徑黑色節(jié)點(diǎn)個數(shù)相同。

2.如果u節(jié)點(diǎn)存在，則其一定是黑色的，那么cur節(jié)點(diǎn)原來的顏色一定是黑色的，現(xiàn)在看到其是紅色的原因是因?yàn)閏ur的子樹在調(diào)整的過程中將cur節(jié)點(diǎn)的顏色由黑色改成紅色。

p為g的左孩子，cur為p的左孩子，則進(jìn)行右單旋轉(zhuǎn)；

p為g的右孩子，cur為p的右孩子，則進(jìn)行左單旋轉(zhuǎn)。

p變黑，g變紅。

情況三: cur為紅，p為紅，g為黑，u不存在/u為黑

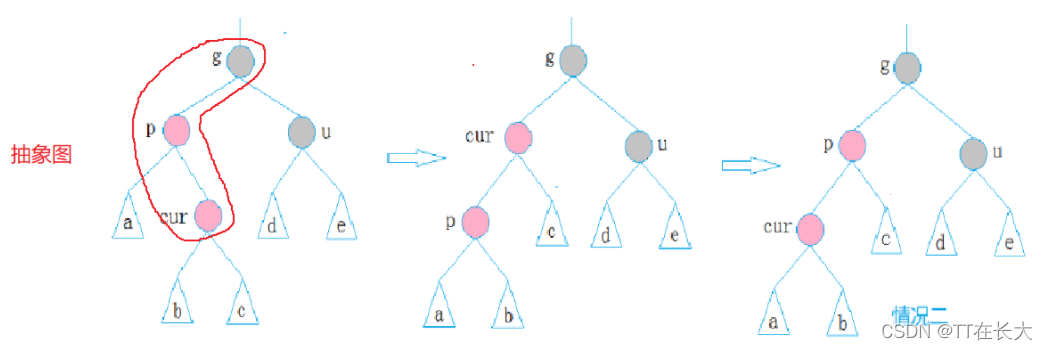
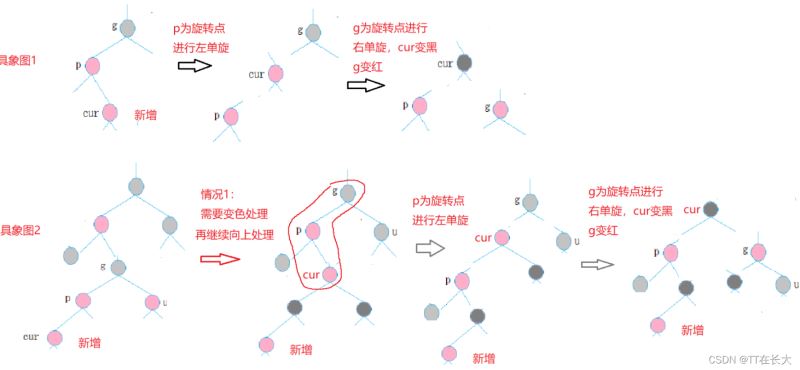
需要進(jìn)行雙旋。

代碼實(shí)現(xiàn)：

while (parent && parent->_col == RED)		//違反規(guī)則三
		{
			Node* grandfather = parent->_parent;

			if (parent == grandfather->_left)			//左半邊
			{
				Node* uncle = parent->_right;

				if (uncle && uncle->_col == red)		//情況一
				{
					uncle->_col = BLACK;
					grandfather->_col = RED;
					parent->_col = BLACK;

					cur = grandfather;			//迭代
					parent = cur->_parent;
				}
				else							//情況2.3
				{
					if (cur == parent->_left)		//單側(cè)
					{
						RotateR(grandfather);

						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else					//折
					{
						RotateL(parent);
						RotateR(grandfather);

						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;		//黑色數(shù)量無變化，不需要向上
				}
			}
			else         // parent == grandfather->_right
			{
				Node* uncle = parent->_left;
				if (uncle && uncle->_col == red)		//情況一
				{
					uncle->_col = BLACK;
					grandfather->_col = RED;
					parent->_col = BLACK;

					cur = grandfather;			//迭代
					parent = cur->_parent;
				}
				else							//情況2.3
				{
					if (cur == parent->_right)		//單側(cè)
					{
						RotateL(grandfather);

						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else					//折
					{
						RotateR(parent);
						RotateL(grandfather);

						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

六、代碼

#pragma once
#include<iostream>
#include<assert.h>

using namespace std;

enum Colour		//紅黑樹顏色枚舉
{
	RED,
	BLACK,
};

template<class K, class V>
struct RBTreeNode					//節(jié)點(diǎn)結(jié)構(gòu)體
{
	RBTreeNode<K, V>* _left;		//左子樹
	RBTreeNode<K, V>* _right;		//右子樹
	RBTreeNode<K, V>* _parent;		//父節(jié)點(diǎn)

	pair<K, V> _kv;

	Colour _col;

	RBTreeNode(const pair<K, V>& kv)	//構(gòu)造函數(shù)
		: _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)
	{}
};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
private:
	Node* _root;

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* parentP = parent->_parent;

		if (subLR)							//左子樹的右子樹連接到父的右
			subLR->_parent = parent;

		parent->_left = subLR;
		subL->_right = parent;
		parent->_parent = subL;

		// 如果parent是根節(jié)點(diǎn)，根新指向根節(jié)點(diǎn)的指針
		if (parent == _root)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			// 如果parent是子樹，可能是其雙親的左子樹，也可能是右子樹
			if (parentP->_left == parent)
				parentP->_left = subL;
			else
				parentP->_right = subL;

			subL->_parent = parentP;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* parentP = parent->_parent;

		if (subRL)
			subRL->_parent = parent;

		parent->_right = subRL;
		subR->_left = parent;
		parent->_parent = subR;

		// 如果parent是根節(jié)點(diǎn)，根新指向根節(jié)點(diǎn)的指針
		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			// 如果parent是子樹，可能是其雙親的左子樹，也可能是右子樹
			if (parentP->_left == parent)
				parentP->_left = subR;
			else
				parentP->_right = subR;

			subR->_parent = parentP;
		}
	}

	void _Destory(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_Destory(root->_left);
		_Destory(root->_right);

		delete root;
	}

public:
	RBTree()
		:_root(nullptr)
	{}

	~RBTree()
	{
		_Destory(_root);
		_root = nullptr;
	}

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first > key)
			{
				cur = cur->_left;
			}
			else if (cur->_kv < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}

		return nullptr;
	}

	pair<Node*, bool> Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return make_pair(_root, true);
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return make_pair(cur, false);
			}
		}

		Node* newNode = new Node(kv);
		newNode->_col = RED;
		if (parent->_kv.first > kv.first)
		{
			parent->_left = newNode;
			newNode->_parent = parent;
		}
		else
		{
			parent->_right = newNode;
			newNode->_parent = parent;
		}
		cur = newNode;

		while (parent && parent->_col == RED)		//違反規(guī)則三
		{
			Node* grandfather = parent->_parent;

			if (parent == grandfather->_left)			//左半邊
			{
				Node* uncle = parent->_right;

				if (uncle && uncle->_col == red)		//情況一
				{
					uncle->_col = BLACK;
					grandfather->_col = RED;
					parent->_col = BLACK;

					cur = grandfather;			//迭代
					parent = cur->_parent;
				}
				else							//情況2.3
				{
					if (cur == parent->_left)		//單側(cè)
					{
						RotateR(grandfather);

						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else					//折
					{
						RotateL(parent);
						RotateR(grandfather);

						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;		//黑色數(shù)量無變化，不需要向上
				}
			}
			else         // parent == grandfather->_right
			{
				Node* uncle = parent->_left;
				if (uncle && uncle->_col == red)		//情況一
				{
					uncle->_col = BLACK;
					grandfather->_col = RED;
					parent->_col = BLACK;

					cur = grandfather;			//迭代
					parent = cur->_parent;
				}
				else							//情況2.3
				{
					if (cur == parent->_right)		//單側(cè)
					{
						RotateL(grandfather);

						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else					//折
					{
						RotateR(parent);
						RotateL(grandfather);

						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;		//插入結(jié)束再次將根變?yōu)楹?

		return make_pair(newNode, true);
	}
};

總結(jié)

本文對紅黑樹進(jìn)行了介紹，并對構(gòu)造，插入，查找進(jìn)行了模擬實(shí)現(xiàn)。

以上就是C++ STL容器詳解之紅黑樹部分模擬實(shí)現(xiàn)的詳細(xì)內(nèi)容，更多關(guān)于C++ STL紅黑樹實(shí)現(xiàn)的資料請關(guān)注服務(wù)器之家其它相關(guān)文章！

原文鏈接：https://blog.csdn.net/RMA515T/article/details/121654417