本文實例講述了Python模擬隨機游走圖形效果。分享給大家供大家參考,具體如下:
在python中,可以利用數組操作來模擬隨機游走。
下面是一個單一的200步隨機游走的例子,從0開始,步長為1和-1,且以相等的概率出現。純Python方式實現,使用了內建的 random 模塊:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
# 隨機游走import matplotlib.pyplot as pltimport randomposition = 0walk = [position]steps = 200for i in range(steps): step = 1 if random.randint(0, 1) else -1 position += step walk.append(position)fig = plt.figure()plt.title("www.zyiz.net")ax = fig.add_subplot(111)ax.plot(walk)plt.show() |
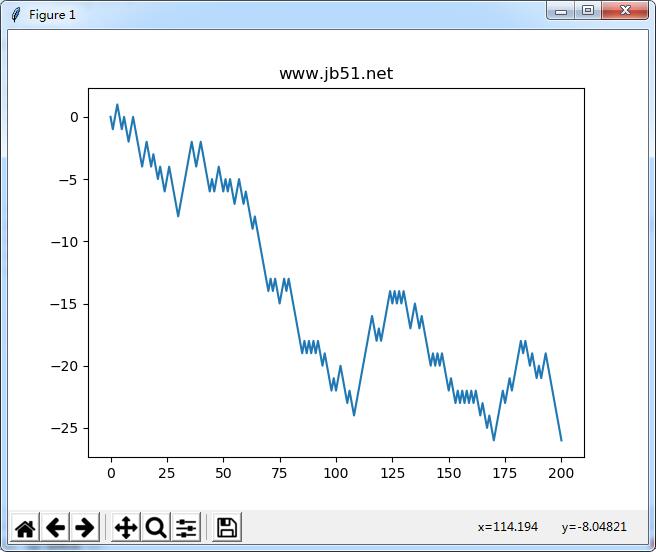
第二種方式:簡單的把隨機步長累積起來并且可以可以使用一個數組表達式來計算。因此,我用 np.random 模塊去200次硬幣翻轉,設置它們為1和-1,并計算累計和:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
# 隨機游走import matplotlib.pyplot as pltimport numpy as npnsteps = 200draws = np.random.randint(0, 2, size=nsteps)steps = np.where(draws > 0, 1, -1)walk = steps.cumsum()fig = plt.figure()plt.title("www.zyiz.net")ax = fig.add_subplot(111)ax.plot(walk)plt.show() |
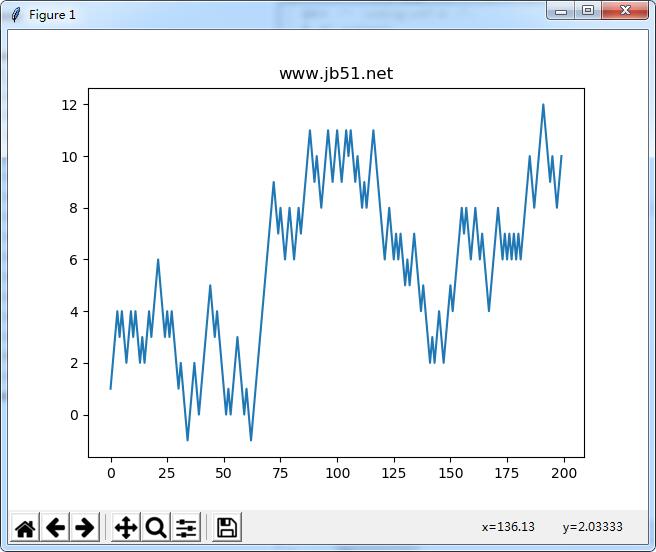
一次模擬多個隨機游走
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
# 隨機游走import matplotlib.pyplot as pltimport numpy as npnwalks = 5nsteps = 200draws = np.random.randint(0, 2, size=(nwalks, nsteps)) # 0 or 1steps = np.where(draws > 0, 1, -1)walks = steps.cumsum(1)fig = plt.figure()plt.title("www.zyiz.net")ax = fig.add_subplot(111)for i in range(nwalks): ax.plot(walks[i])plt.show() |
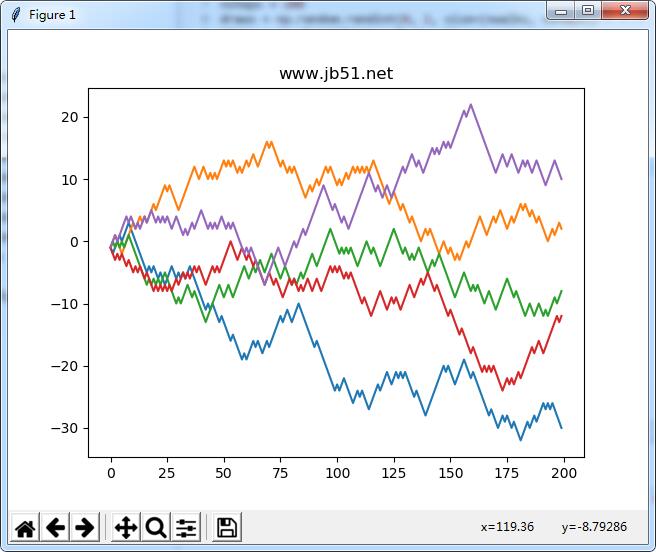
當然,還可以大膽的試驗其它的分布的步長,而不是相等大小的硬幣翻轉。你只需要使用一個不同的隨機數生成函數,如 normal 來產生相同均值和標準偏差的正態分布:
|
1
|
steps = np.random.normal(loc=0, scale=0.25, size=(nwalks, nsteps)) |
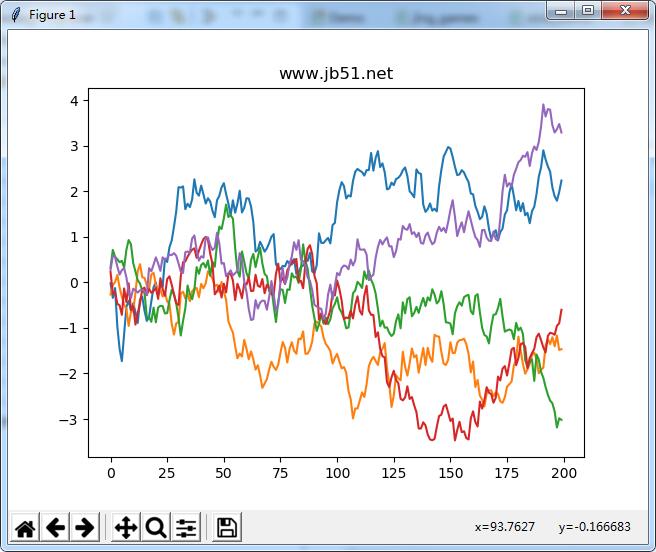
希望本文所述對大家Python程序設計有所幫助。
原文鏈接:http://www.cnblogs.com/hhh5460/p/4356635.html










