本文主要研究的是Python機器學習logistic回歸的相關內容,同時介紹了一些機器學習中的概念,具體如下。
Logistic回歸的主要目的:尋找一個非線性函數sigmod最佳的擬合參數
擬合、插值和逼近是數值分析的三大工具
回歸:對一直公式的位置參數進行估計
擬合:把平面上的一些系列點,用一條光滑曲線連接起來
logistic主要思想:根據現有數據對分類邊界線建立回歸公式、以此進行分類
sigmoid函數:在神經網絡中它是所謂的激勵函數。當輸入大于0時,輸出趨向于1,輸入小于0時,輸出趨向0,輸入為0時,輸出為0.5

梯度上升:要找到某個函數的最大值,最好的方法是沿著該函數的梯度方向探尋
收斂:隨著迭代的運行算法的結果和真實結果的誤差越來越小,且趨向于一個固定值。
爬山算法:是完完全全的貪心算法,每次鼠目寸光的選擇一個當前最優解,英雌只能搜尋到局部最優值
模擬退火算法:也是一種貪心算法但它的sou索過程引入了隨機因素,模擬退火算法以一定的概念來接受一個比當前解要差的解,因此有可能會跳出這個局部最優解,達到全局最優解。
處理數據中的缺失值:
使用可用特征的均值來填補缺失值
使用特殊值來填補缺失值,如-1
忽略有缺失值的樣本
使用相似樣本的均值添補缺失值
使用其它機器學習算法預測缺失值
標簽與特征不同,很難確定采用某個合適的值來替換。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
|
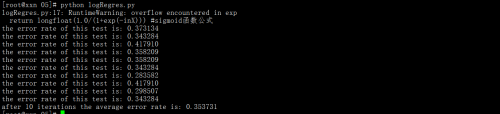
#coding:utf-8 from numpy import *import math def loadDataSet(): dataMat = []; labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat,labelMat def sigmoid(inX): return longfloat(1.0/(1+exp(-inX))) #sigmoid函數公式 def gradAscent(dataMatIn, classLabels): #dataMatIn 一個2維的數組;classLabels 類別標簽 dataMatrix = mat(dataMatIn) #轉換為矩陣 labelMat = mat(classLabels).transpose() #得到矩陣的轉置矩陣 m,n = shape(dataMatrix) #讀取矩陣的長度,二維矩陣,返回兩個值 alpha = 0.001 #向目標移動的步長 maxCycles = 500 #迭代次數 weights = ones((n,1)) #ones()函數用以創建指定形狀和類型的數組,默認情況下返回的類型是float64。但是,如果使用ones()函數時指定了數據類型,那么返回的就是該類型 for k in range(maxCycles): h = sigmoid(dataMatrix*weights) #matrix mult error = (labelMat - h) #vector subtraction weights = weights + alpha * dataMatrix.transpose()* error #matrix mult return weights def plotBestFit(weights): import matplotlib as mpl mpl.use('Agg') #為了防止出現:RuntimeError: could not open display報錯 import matplotlib.pyplot as plt dataMat,labelMat=loadDataSet() dataArr = array(dataMat) n = shape(dataArr)[0] xcord1 = []; ycord1 = [] xcord2 = []; ycord2 = [] for i in range(n): if int(labelMat[i])== 1: xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) else: xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) fig = plt.figure() #figure: 控制dpi、邊界顏色、圖形大小、和子區( subplot)設置 ax = fig.add_subplot(111) # 參數111的意思是:將畫布分割成1行1列,圖像畫在從左到右從上到下的第1塊, ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') ax.scatter(xcord2, ycord2, s=30, c='green') x = arange(-3.0, 3.0, 0.1) y = (-weights[0]-weights[1]*x)/weights[2] ax.plot(x, y) plt.xlabel('X1'); plt.ylabel('X2'); plt.savefig('plotBestFit.png') #因為我是騰訊云服務器,沒有圖形界面,所以我保存為圖片。 #隨機梯度上升算法def stocGradAscent0(dataMatrix, classLabels): m,n = shape(dataMatrix) alpha = 0.01 weights = ones(n) #initialize to all ones for i in range(m): h = sigmoid(sum(dataMatrix[i]*weights)) error = classLabels[i] - h weights = weights + alpha * error * dataMatrix[i] #回歸系數的更新操作 return weights #改進的隨機梯度上升算法def stocGradAscent1(dataMatrix, classLabels, numIter=150): #較之前的增加了一個迭代次數作為第三個參數,默認值150 m,n = shape(dataMatrix) weights = ones(n) for j in range(numIter): dataIndex = range(m) for i in range(m): alpha = 4/(1.0+j+i)+0.0001 randIndex = int(random.uniform(0,len(dataIndex))) #樣本隨機選擇 h = sigmoid(sum(dataMatrix[randIndex]*weights)) error = classLabels[randIndex] - h weights = weights + alpha * error * dataMatrix[randIndex] #回歸系數的更新操作 del(dataIndex[randIndex]) return weights #以回歸系數和特征向量作為輸入計算對應的sigmoid值def classifyVector(inX, weights): prob = sigmoid(sum(inX*weights)) if prob > 0.5: return 1.0 #如果sigmoid值大于0.5函數返回1,否則返回0 else: return 0.0 #打開測試集和訓練集,并對數據進行格式化處理的函數def colicTest(): frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt') trainingSet = []; trainingLabels = [] for line in frTrain.readlines(): currLine = line.strip().split('\t') lineArr =[] for i in range(21): lineArr.append(float(currLine[i])) trainingSet.append(lineArr) trainingLabels.append(float(currLine[21])) trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000) #計算回歸系數向量 errorCount = 0; numTestVec = 0.0 for line in frTest.readlines(): numTestVec += 1.0 currLine = line.strip().split('\t') lineArr =[] for i in range(21): lineArr.append(float(currLine[i])) if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]): errorCount += 1 errorRate = (float(errorCount)/numTestVec) print "the error rate of this test is: %f" % errorRate return errorRate#調用函數colicTest()10次,并求結果的平均值def multiTest(): numTests = 10; errorSum=0.0 for k in range(numTests): errorSum += colicTest() print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)) |

總結
以上就是本文關于Python機器學習logistic回歸代碼解析的全部內容,希望對大家有所幫助。感興趣的朋友可以繼續參閱本站其他相關專題,如有不足之處,歡迎留言指出。感謝朋友們對本站的支持!
原文鏈接:http://blog.51cto.com/9399369/1958200










