我就廢話不多說了,大家還是直接看代碼吧~
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
import kerasimport numpy as npimport matplotlib.pyplot as plt#Sequential 按順序構成的模型from keras.models import Sequential#Sequential是模型結構,輸入層,隱藏層,輸出層#Dense 全連接層,Activation激活函數from keras.layers import Dense,Activationfrom keras.optimizers import SGD x_data=np.linspace(-0.5,0.5,200)#從-0.5到0.5范圍內生成200個隨機點noise=np.random.normal(0,0.02,x_data.shape)#生成和x_data形狀一樣的噪聲y_data=np.square(x_data)+noise #顯示隨機點#plt.scatter(x_data,y_data)#plt.show() #構建一個順序模型model=Sequential() #1-10-1,添加一個隱藏層model.add(Dense(units=10,input_dim=1,activation='relu'))#units是隱藏層,輸出維度,輸出y,input_dim是輸入維度,輸入x#model.add(Activation('tanh'))#給這一層添加一個雙曲正切激活函數tanh函數model.add(Dense(units=1,input_dim=10,activation='relu'))#input_dim可以不寫,它可以識別到上一句的輸出是10維#model.add(Activation('tanh'))#給這一層添加一個雙曲正切激活函數tanh函數#定義優化器sgd=SGD(lr=0.3)#學習率提高到0.3,訓練速度會加快 model.compile(optimizer=sgd,loss='mse')#編譯這個模型,sgd是隨機梯度下降法,優化器.mse是均方誤差 #訓練模型for step in range(5001): #每次訓練一個批次 cost=model.train_on_batch(x_data,y_data)#代價函數的值,其實就是loss #每500個batch打印一次cost值 if step %500==0: print('cost:',cost) #打印權值和偏置值W,b=model.layers[0].get_weights()#線性回歸,只有一層print('W:',W,'b:',b) #x_data輸入網絡中,得到預測值y_predy_pred=model.predict(x_data) #顯示隨機點splt.scatter(x_data,y_data)#顯示預測結果plt.plot(x_data,y_pred,'r-',lw=3)#r-表示紅色的線,lw表示線寬plt.show() |
結果:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
cost: 0.0077051604cost: 0.0004980223cost: 0.00047812634cost: 0.00047762066cost: 0.00047761563cost: 0.00047761557cost: 0.0004776156cost: 0.0004776156cost: 0.0004776156cost: 0.00047761566cost: 0.0004776156W: [[ 0.37828678 0.37509003 0.1847014 -0.46519393 -0.6347979 -0.70865685 0.55382997 -0.66780925 0.08229994 0.5980157 ]] b: [-0.00412499 -0.01216194 0.01939214 -0.03005166 -0.00475936 -0.00794064 -0.00015427 -0.01620528 0.08056344 -0.01741577] |
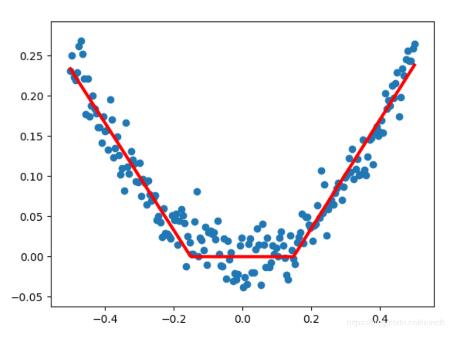
以上這篇使用keras實現非線性回歸(兩種加激活函數的方式)就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持服務器之家。
原文鏈接:https://blog.csdn.net/iamcfb_/article/details/87461442