本文實(shí)例講述了Python利用全連接神經(jīng)網(wǎng)絡(luò)求解MNIST問題。分享給大家供大家參考,具體如下:
1、單隱藏層神經(jīng)網(wǎng)絡(luò)
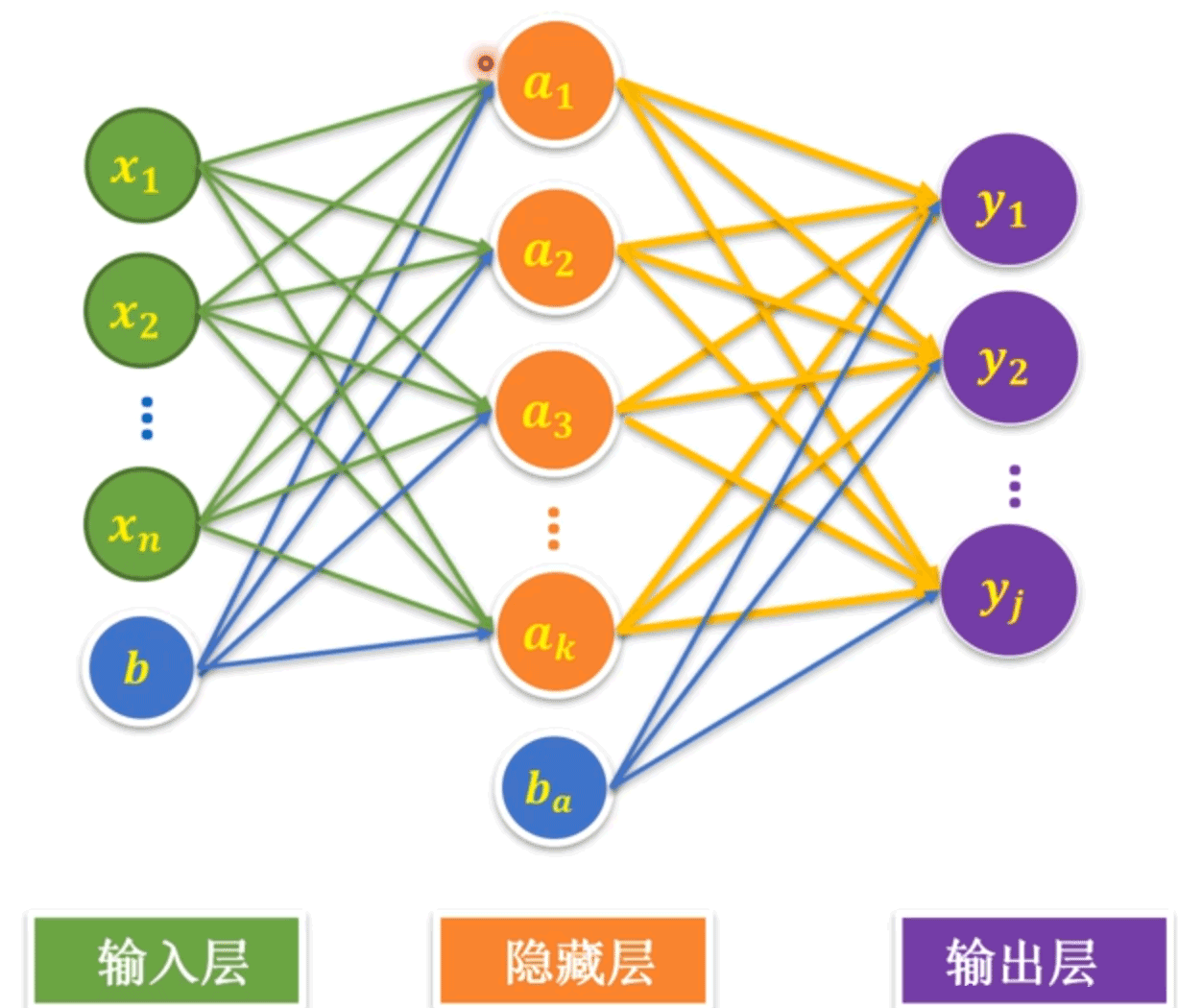
人類的神經(jīng)元在樹突接受刺激信息后,經(jīng)過細(xì)胞體處理,判斷如果達(dá)到閾值,則將信息傳遞給下一個(gè)神經(jīng)元或輸出。類似地,神經(jīng)元模型在輸入層輸入特征值x之后,與權(quán)重w相乘求和再加上b,經(jīng)過激活函數(shù)判斷后傳遞給下一層隱藏層或輸出層。
單神經(jīng)元的模型只有一個(gè)求和節(jié)點(diǎn)(如左下圖所示)。全連接神經(jīng)網(wǎng)絡(luò)(Full Connected Networks)如右下圖所示,中間層有多個(gè)神經(jīng)元,并且每層的每個(gè)神經(jīng)元都是與上一層和下一層的節(jié)點(diǎn)都對(duì)應(yīng)連接。中間隱藏層只有一層的神經(jīng)元網(wǎng)絡(luò)稱為單隱藏層神經(jīng)網(wǎng)絡(luò)。如果有多個(gè)中間隱藏層則稱為多隱藏層神經(jīng)網(wǎng)絡(luò)。

常見的激活函數(shù)如下所示:
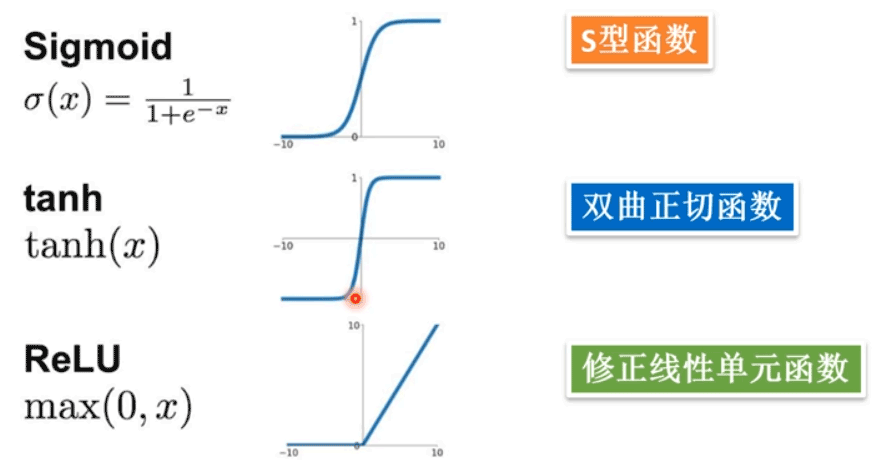
下面是在單個(gè)神經(jīng)元邏輯回歸求解MNIST手寫數(shù)字識(shí)別問題的基礎(chǔ)上,采用單隱藏層神經(jīng)網(wǎng)絡(luò)進(jìn)行求解的過程。
首先載入數(shù)據(jù),從Tensor FLow提供的數(shù)據(jù)庫中導(dǎo)入MNIST數(shù)據(jù)
|
1
2
3
|
import tensorflow as tfimport tensorflow.examples.tutorials.mnist.input_data as input_datamnist=input_data.read_data_sets('MNIST_data/',one_hot=True) |
構(gòu)建輸入層,其中x是圖像的特征值,由于是28×28=784個(gè)像素點(diǎn),所有輸入為未知行數(shù)、每行784的二維數(shù)組。y是圖像的標(biāo)簽值,共有0~9十種可能,所有為[None,10]的二維數(shù)組
|
1
2
|
x=tf.placeholder(tf.float32,[None,784],name='x')y=tf.placeholder(tf.float32,[None,10],name='y') |
構(gòu)建隱藏層,設(shè)置隱藏層神經(jīng)元個(gè)數(shù)為256,由于輸入層輸入為784,而隱藏層神經(jīng)元為h1_num,所以W1為[784,h1_num]形式的二維數(shù)組,b為[h1_num]的一維向量。此外采用ReLU作為激活函數(shù)處理輸出。
|
1
2
3
4
|
h1_num=256 #設(shè)置隱藏層神經(jīng)元數(shù)量W1=tf.Variable(tf.random_normal([784,h1_num]),name='W1')b1=tf.Variable(tf.zeros([h1_num]),name='b1')Y1=tf.nn.relu(tf.matmul(x,W1)+b1) #激活函數(shù) |
構(gòu)建輸出層,由于隱藏層有h1_num個(gè)神經(jīng)元輸出,輸出層輸出10種輸出結(jié)果,所以W2為[h1_num,10]的二維數(shù)組,b2為[10]的一維向量。最后結(jié)果通過softmax將線性輸出Y2轉(zhuǎn)化為獨(dú)熱編碼方式。
|
1
2
3
4
|
W2=tf.Variable(tf.random_normal([h1_num,10]),name='W2')b2=tf.Variable(tf.zeros([10]),name='b2')Y2=tf.matmul(Y1,W2)+b2pred=tf.nn.softmax(Y2) |
設(shè)置訓(xùn)練的超參數(shù)、損失函數(shù)、優(yōu)化器,這里采用Adam Optimizer進(jìn)行優(yōu)化。準(zhǔn)確率是通過比較預(yù)測(cè)值和標(biāo)簽值是否一致來定義。在定義損失函數(shù)時(shí),如果直接使用交叉熵的方式定義,會(huì)出現(xiàn)log0值為NaN的情況,導(dǎo)致數(shù)據(jù)不穩(wěn)定,無法得出結(jié)果。Tensor Flow提供了結(jié)合softmax定義交叉熵的方式softmax_cross_entropy_with_logits(),第一個(gè)參數(shù)為不經(jīng)softmax處理的前向計(jì)算結(jié)果Y2,第二個(gè)參數(shù)為標(biāo)簽值y
|
1
2
3
4
5
6
7
8
9
10
11
|
train_epochs=20 #訓(xùn)練輪數(shù)batch_size=50 #每個(gè)批次的樣本數(shù)batch_num=int(mnist.train.num_examples/batch_size) #一輪需要訓(xùn)練多少批learning_rate=0.01#定義損失函數(shù)、優(yōu)化器loss_function=tf.reduce_mean( #softmax交叉熵?fù)p失函數(shù) tf.nn.softmax_cross_entropy_with_logits(logits=Y2,labels=y)) optimizer=tf.train.AdamOptimizer(learning_rate).minimize(loss_function)#定義準(zhǔn)確率correct_prediction=tf.equal(tf.argmax(pred,1),tf.argmax(y,1))accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) |
進(jìn)行訓(xùn)練并輸出損失值與準(zhǔn)確率,訓(xùn)練進(jìn)行多輪,每輪一開始分批次讀入數(shù)據(jù)進(jìn)行訓(xùn)練,每結(jié)束一輪輸出一次損失和準(zhǔn)確率。
|
1
2
3
4
5
6
7
8
9
10
11
12
|
ss=tf.Session()ss.run(tf.global_variables_initializer()) #進(jìn)行全部變量的初始化 for epoch in range(train_epochs): for batch in range(batch_num): #分批次讀取數(shù)據(jù)進(jìn)行訓(xùn)練 xs,ys=mnist.train.next_batch(batch_size) ss.run(optimizer,feed_dict={x:xs,y:ys}) loss,acc=ss.run([loss_function,accuracy],\ feed_dict={x:mnist.validation.images,y:mnist.validation.labels}) print('第%2d輪訓(xùn)練:損失為:%9f,準(zhǔn)確率:%.4f'%(epoch+1,loss,acc)) ss.close() |
運(yùn)行結(jié)果如下圖,與單個(gè)神經(jīng)元相比,可以較快得到較高的準(zhǔn)確率
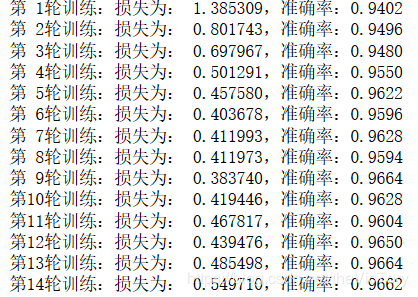
評(píng)估模型,將測(cè)試集數(shù)據(jù)填充入占位符x,y去求準(zhǔn)確率,
|
1
2
|
test_res=ss.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels})print('測(cè)試集的準(zhǔn)確率為:%.4f'%(test_res)) |
2、多層神經(jīng)網(wǎng)絡(luò)
多層是指中間的隱藏層有多個(gè),例如使用兩層隱藏層,第一個(gè)隱藏層在計(jì)算后將結(jié)果輸出到第二個(gè)隱藏層,再由第二個(gè)隱藏層計(jì)算后交給輸出層,而第二個(gè)隱藏層的設(shè)置與第一個(gè)基本相同,例如:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#構(gòu)建輸入層x=tf.placeholder(tf.float32,[None,784],name='x')y=tf.placeholder(tf.float32,[None,10],name='y')#構(gòu)建第一個(gè)隱藏層h1_num=256 #第一隱藏層神經(jīng)元數(shù)量256W1=tf.Variable(tf.truncated_normal([784,h1_num],stddev=0.1),name='W1')b1=tf.Variable(tf.zeros([h1_num]),name='b1')Y1=tf.nn.relu(tf.matmul(x,W1)+b1)#構(gòu)建第二個(gè)隱藏層h2_num=64 #第二隱藏層神經(jīng)元數(shù)量64W2=tf.Variable(tf.random_normal([h1_num,h2_num],stddev=0.1),name='W2')b2=tf.Variable(tf.zeros([h2_num]),name='b2')Y2=tf.nn.relu(tf.matmul(Y1,W2)+b2)#構(gòu)建輸出層W3=tf.Variable(tf.random_normal([h2_num,10],stddev=0.1),name='W3')b3=tf.Variable(tf.zeros([10]),name='b3')Y3=tf.matmul(Y2,W3)+b3pred=tf.nn.softmax(Y3) |
在第一隱藏層產(chǎn)生參數(shù)W1時(shí)采用的是截?cái)嗾龖B(tài)分布的隨機(jī)函數(shù)tf.truncated_normal(),與普通正太分布相比,截?cái)嗾龖B(tài)分布生成的值之間的差距不會(huì)太大。
設(shè)置的第一隱藏層的神經(jīng)元256個(gè),第二層64個(gè),因此第二層的每個(gè)輸入有256個(gè)特征值,并產(chǎn)生64個(gè)輸出,相應(yīng)的W2的shape為[h1_num,h2_num],b2的shape為[h2_num]。輸出層W3的shape為[h2_num,10]。函數(shù)的其他部分與單層神經(jīng)網(wǎng)絡(luò)相同。
經(jīng)過運(yùn)算多層的神經(jīng)網(wǎng)絡(luò)訓(xùn)練的準(zhǔn)確率不一定比單層的高,因?yàn)檫€涉及到訓(xùn)練的超參數(shù)的設(shè)置等多種因素。但是多層神經(jīng)網(wǎng)絡(luò)的運(yùn)行速度比單層慢,越多層的神經(jīng)網(wǎng)絡(luò)意味著更加復(fù)雜的計(jì)算量。
全連接層函數(shù)
通過以上多層神經(jīng)網(wǎng)絡(luò)的定義可以看出兩個(gè)隱藏層與輸出層的構(gòu)建方法基本類似,都是定義對(duì)應(yīng)的變量W、b,在定義W時(shí)其shape為[輸出維度,輸出維度],因此可以將隱藏層與輸出層統(tǒng)一定義為一個(gè)全連接層函數(shù):
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#定義一個(gè)通用的全連接層函數(shù)模型def fcn_layer(inputs,in_dim,out_dim,activation=None): W=tf.Variable(tf.truncated_normal([in_dim,out_dim],stddev=0.1)) b=tf.Variable(tf.zeros([out_dim])) Y=tf.matmul(inputs,W)+b if activation==None: output=Y else: output=activation(Y) return output#構(gòu)建第一個(gè)隱藏層Y1=fcn_layer(x,784,256,tf.nn.relu)#構(gòu)建第二個(gè)隱藏層Y2=fcn_layer(Y1,256,64,tf.nn.relu)#構(gòu)建輸出層Y3=fcn_layer(Y2,64,10)pred=tf.nn.softmax(Y3) |
其中inputs為本層的輸入,in_dim為本層的輸入維度,也就是上一層的輸出維度,out_dim為本層的輸出維度,activation為激活函數(shù),默認(rèn)為None。將輸入與權(quán)重W叉乘再加上偏置值b得到Y(jié),如果定義了激活函數(shù),用激活函數(shù)處理Y,否則直接將Y賦給output輸出。
3、模型的保存與讀取
在模型訓(xùn)練結(jié)束后,如果希望下次繼續(xù)使用或訓(xùn)練模型則需要將儲(chǔ)存起來。
模型的儲(chǔ)存
首先需要定義模型數(shù)據(jù)的保存路徑:
|
1
2
3
4
|
import ossave_dir='D:/Temp/MachineLearning/ModelSaving/' #定義模型的保存路徑if not os.path.exists(save_dir): #如果不存在該路徑則創(chuàng)建 os.makedirs(save_dir) |
定義儲(chǔ)存粒度與saver,所謂儲(chǔ)存粒度即每個(gè)幾輪數(shù)據(jù)進(jìn)行一次儲(chǔ)存
|
1
2
3
|
save_step=5 #定義存儲(chǔ)粒度 saver=tf.train.Saver() #定義saver |
在每輪訓(xùn)練結(jié)束后進(jìn)行判斷,每隔5輪儲(chǔ)存一次,儲(chǔ)存路徑中拼接輪數(shù)信息,
|
1
2
|
if epoch%save_step==0: saver.save(ss,os.path.join(save_dir,'mnist_fcn_{:02d}.ckpt'.format(epoch+1))) |
在所有迭代訓(xùn)練執(zhí)行結(jié)束后,再整體儲(chǔ)存一次
|
1
|
saver.save(ss,os.path.join(save_dir,'mnist_fcn.ckpt')) |
這樣就會(huì)在指定目錄下生成模型的保存文件:
模型的讀取
從定義的模型目錄中讀取存盤點(diǎn)數(shù)據(jù),并將其中的參數(shù)賦值給當(dāng)前的session,然后便可以直接利用session進(jìn)行測(cè)試,其準(zhǔn)確率與保存時(shí)一致。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
save_dir='D:/Temp/MachineLearning/ModelSaving/' #定義模型的保存路徑saver=tf.train.Saver() #定義saver ss=tf.Session()ss.run(tf.global_variables_initializer()) ckpt=tf.train.get_checkpoint_state(save_dir) #讀取存盤點(diǎn)if ckpt and ckpt.model_checkpoint_path: saver.restore(ss,ckpt.model_checkpoint_path) #從存盤中恢復(fù)參數(shù)到當(dāng)前的session print('數(shù)據(jù)恢復(fù)從',ckpt.model_checkpoint_path) test_res=accuracy.eval(session=ss,feed_dict={x:mnist.test.images,y:mnist.test.labels})print('測(cè)試集的準(zhǔn)確率為:%.4f'%(test_res)) |
在讀取模型時(shí)有時(shí)候會(huì)遇到報(bào)錯(cuò):
|
1
|
NotFoundError (see above for traceback): Restoring from checkpoint failed. This is most likely due to a Variable name or other graph key that is missing from the checkpoint. Please ensure that you have not altered the graph expected based on the checkpoint. |
這時(shí)只需重啟kernel即可。
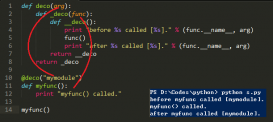
通過圖來保存模型
也可以將訓(xùn)練好的模型以圖的形式保存為.pb文件,下次直接可以使用,但不可以繼續(xù)訓(xùn)練。
通過tf.train.write_graph函數(shù)來保存模型如下:
|
1
2
3
4
5
6
|
import tensorflow as tf v=tf.Variable(1.0,'new_var')with tf.Session() as ss: tf.train.write_graph(ss.graph_def,'D:\Temp\MachineLearning\ModelSaving\Graph', 'test_graph.pb',as_text=False) |
讀取圖文件并還原:
|
1
2
3
4
5
6
7
|
with tf.Session() as ss: with tf.gfile.GFile('D:/Temp\MachineLearning/ModelSaving/Graph/test_graph.pb','rb') as pb_file: graph_def=tf.GraphDef() graph_def.ParseFromString(pb_file.read()) ss.graph.as_default() tf.import_graph_def(graph_def) print(graph_def) |
希望本文所述對(duì)大家Python程序設(shè)計(jì)有所幫助。
原文鏈接:https://blog.csdn.net/theVicTory/article/details/95768702