在學習線性代數時我們所接觸的矩陣之間的乘法是矩陣的叉乘,有這樣一個前提:
若矩陣A是m*n階的,B是p*q階的矩陣,AB能相乘,首先得滿足:n=p,即A的列數要等于B的行數。運算的方法如下圖:
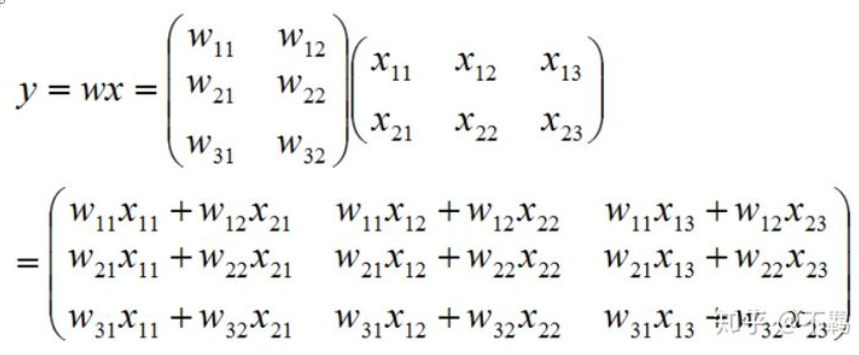
當時學線性代數時老師教的更為直觀記法:
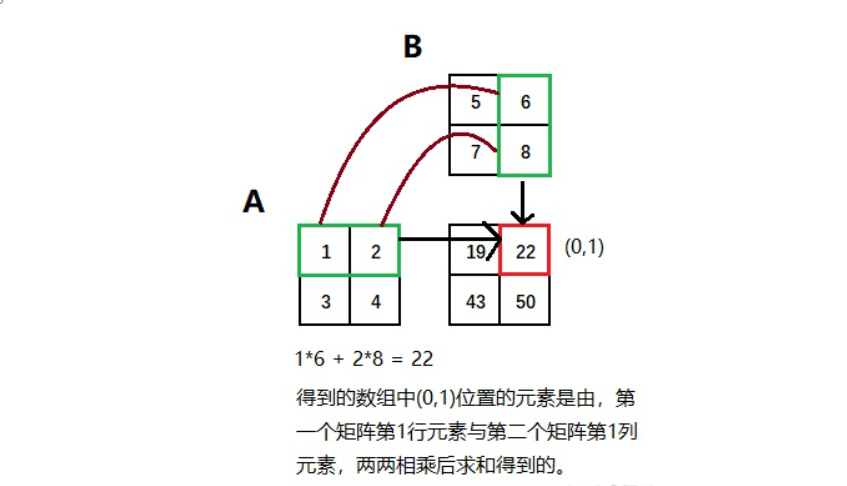
點乘則是這樣:

假如有a,b兩個矩陣,在Matlab中我們實現點乘和叉乘的方式分別如下:
|
1
2
|
a.*b %表示點乘a*b %表示叉乘 |
下面我們來看看python中的操作:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
import numpy as npa = np.arange(1, 10).reshape(3, 3)b = np.arange(1, 10).reshape(3, 3)print(a)print(a*b) # 點乘只允許1*m和m*na1 = np.mat(np.arange(1, 10).reshape(3, 3))a2 = np.mat(np.arange(1, 10).reshape(3, 3))a3 = np.dot(a1, a2) # 叉乘使用dotprint(a1)print(a3) |
運行結果:
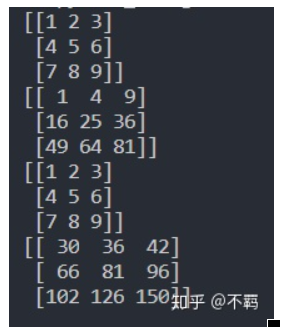
使用python操作剛好與Matlab相反,使用點乘計算實際上是各數組相同下標相乘。Numpy庫中的dot函數則是為了實現數組相乘。
到此這篇關于Python中的Numpy 矩陣運算的文章就介紹到這了,更多相關Python Numpy 矩陣運算內容請搜索服務器之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持服務器之家!
原文鏈接:https://zhuanlan.zhihu.com/p/113863268










