[LeetCode] 52. N-Queens II N皇后問題之二
The n-queens puzzle is the problem of placing nqueens on an n×n chessboard such that no two queens attack each other.
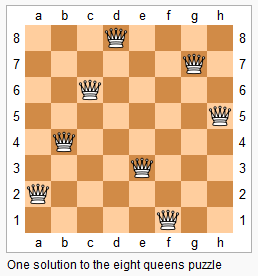
Given an integer n, return the number of distinct solutions to the n-queens puzzle.
Example:
Input: 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown below.
[
[".Q..", // Solution 1
"...Q",
"Q...",
"..Q."],["..Q.", // Solution 2
"Q...",
"...Q",
".Q.."]
]
這道題是之前那道 N-Queens 的延伸,說是延伸其實我覺得兩者順序應該顛倒一樣,上一道題比這道題還要稍稍復雜一些,兩者本質上沒有啥區別,都是要用回溯法 Backtracking 來解,如果理解了之前那道題的思路,此題只要做很小的改動即可,不再需要求出具體的皇后的擺法,只需要每次生成一種解法時,計數器加一即可,代碼如下:
解法一:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {public: int totalNQueens(int n) { int res = 0; vector<int> pos(n, -1); helper(pos, 0, res); return res; } void helper(vector<int>& pos, int row, int& res) { int n = pos.size(); if (row == n) ++res; for (int col = 0; col < n; ++col) { if (isValid(pos, row, col)) { pos[row] = col; helper(pos, row + 1, res); pos[row] = -1; } } } bool isValid(vector<int>& pos, int row, int col) { for (int i = 0; i < row; ++i) { if (col == pos[i] || abs(row - i) == abs(col - pos[i])) { return false; } } return true; }}; |
但是其實我們并不需要知道每一行皇后的具體位置,而只需要知道會不會產生沖突即可。對于每行要新加的位置,需要看跟之前的列,對角線,及逆對角線之間是否有沖突,所以我們需要三個布爾型數組,分別來記錄之前的列 cols,對角線 diag,及逆對角線 anti_diag 上的位置,其中 cols 初始化大小為n,diag 和 anti_diag 均為 2n。列比較簡單,是哪列就直接去 cols 中查找,而對角線的話,需要處理一下,如果我們仔細觀察數組位置坐標的話,可以發現所有同一條主對角線的數,其縱坐標減去橫坐標再加n,一定是相等的。同理,同一條逆對角線上的數字,其橫縱坐標之和一定是相等的,根據這個,就可以快速判斷主逆對角線上是否有沖突。任意一個有沖突的話,直接跳過當前位置,否則對于新位置,三個數組中對應位置都賦值為 true,然后對下一行調用遞歸,遞歸返回后記得還要還原狀態,參見代碼如下:
解法二:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {public: int totalNQueens(int n) { int res = 0; vector<bool> cols(n), diag(2 * n), anti_diag(2 * n); helper(n, 0, cols, diag, anti_diag, res); return res; } void helper(int n, int row, vector<bool>& cols, vector<bool>& diag, vector<bool>& anti_diag, int& res) { if (row == n) ++res; for (int col = 0; col < n; ++col) { int idx1 = col - row + n, idx2 = col + row; if (cols[col] || diag[idx1] || anti_diag[idx2]) continue; cols[col] = diag[idx1] = anti_diag[idx2] = true; helper(n, row + 1, cols, diag, anti_diag, res); cols[col] = diag[idx1] = anti_diag[idx2] = false; } }}; |
到此這篇關于C++實現LeetCode(52.N皇后問題之二)的文章就介紹到這了,更多相關C++實現N皇后問題之二內容請搜索服務器之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持服務器之家!
原文鏈接:https://www.cnblogs.com/grandyang/p/4380706.html