[LeetCode] 51. N-Queens N皇后問題
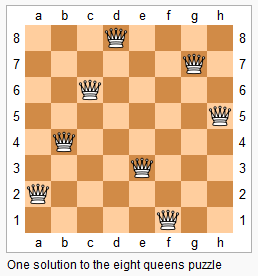
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.
Example:
Input: 4
Output: [
[".Q..", // Solution 1
"...Q",
"Q...",
"..Q."],["..Q.", // Solution 2
"Q...",
"...Q",
".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.
經(jīng)典的N皇后問題,基本所有的算法書中都會包含的問題。可能有些人對國際象棋不太熟悉,大家都知道中國象棋中最叼的是車,橫豎都能走,但是在國際象棋中還有更叼的,就是皇后,不但能橫豎走,還能走兩個斜線,有如 bug 一般的存在。所以經(jīng)典的八皇后問題就應(yīng)運(yùn)而生了,在一個 8x8 大小的棋盤上如果才能放8個皇后,使得兩兩之間不能相遇,所謂一山不能容二虎,而這里有八個母老虎,互相都不能相遇。對于這類問題,沒有太簡便的方法,只能使用窮舉法,就是嘗試所有的組合,每放置一個新的皇后的時候,必須要保證跟之前的所有皇后不能沖突,若發(fā)生了沖突,說明當(dāng)前位置不能放,要重新找地方,這個邏輯非常適合用遞歸來做。我們先建立一個長度為 nxn 的全是點(diǎn)的數(shù)組 queens,然后從第0行開始調(diào)用遞歸。在遞歸函數(shù)中,我們首先判斷當(dāng)前行數(shù)是否已經(jīng)為n,是的話,說明所有的皇后都已經(jīng)成功放置好了,所以我們只要將 queens 數(shù)組加入結(jié)果 res 中即可。否則的話,我們遍歷該行的所有列的位置,行跟列的位置都確定后,我們要驗(yàn)證當(dāng)前位置是否會產(chǎn)生沖突,那么就需要使用一個子函數(shù)來判斷了,首先驗(yàn)證該列是否有沖突,就遍歷之前的所有行,若某一行相同列也有皇后,則沖突返回false;再驗(yàn)證兩個對角線是否沖突,就是一些坐標(biāo)轉(zhuǎn)換,主要不要寫錯了,若都沒有沖突,則說明該位置可以放皇后,放了新皇后之后,再對下一行調(diào)用遞歸即可,注意遞歸結(jié)束之后要返回狀態(tài),參見代碼如下:
解法一:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {public: vector<vector<string>> solveNQueens(int n) { vector<vector<string>> res; vector<string> queens(n, string(n, '.')); helper(0, queens, res); return res; } void helper(int curRow, vector<string>& queens, vector<vector<string>>& res) { int n = queens.size(); if (curRow == n) { res.push_back(queens); return; } for (int i = 0; i < n; ++i) { if (isValid(queens, curRow, i)) { queens[curRow][i] = 'Q'; helper(curRow + 1, queens, res); queens[curRow][i] = '.'; } } } bool isValid(vector<string>& queens, int row, int col) { for (int i = 0; i < row; ++i) { if (queens[i][col] == 'Q') return false; } for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; --i, --j) { if (queens[i][j] == 'Q') return false; } for (int i = row - 1, j = col + 1; i >= 0 && j < queens.size(); --i, ++j) { if (queens[i][j] == 'Q') return false; } return true; }}; |
我們還可以只使用一個一維數(shù)組 queenCol 來保存所有皇后的列位置,初始化均為-1, 那么 queenCol[i] 就是表示第i個皇后在 (i, queenCol[i]) 位置,遞歸函數(shù)還是跟上面的解法相同,就是在當(dāng)前行數(shù)等于n的時候,我們要將 queenCol 還原成一個 nxn 大小的矩陣,并存入結(jié)果 res 中。這種記錄每個皇后的坐標(biāo)的方法在驗(yàn)證沖突的時候比較簡單,只要從第0行遍歷到當(dāng)前行,若跟之前的皇后的列數(shù)相同,直接返回false,叼就叼在判斷對角線沖突非常簡便,因?yàn)楫?dāng)兩個點(diǎn)在同一條對角線上,那么二者的橫坐標(biāo)差的絕對值等于縱坐標(biāo)差的絕對值,利用這條性質(zhì),可以快速的判斷沖突,代碼如下:
解法二:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {public: vector<vector<string>> solveNQueens(int n) { vector<vector<string>> res; vector<int> queenCol(n, -1); helper(0, queenCol, res); return res; } void helper(int curRow, vector<int>& queenCol, vector<vector<string>>& res) { int n = queenCol.size(); if (curRow == n) { vector<string> out(n, string(n, '.')); for (int i = 0; i < n; ++i) { out[i][queenCol[i]] = 'Q'; } res.push_back(out); return; } for (int i = 0; i < n; ++i) { if (isValid(queenCol, curRow, i)) { queenCol[curRow] = i; helper(curRow + 1, queenCol, res); queenCol[curRow] = -1; } } } bool isValid(vector<int>& queenCol, int row, int col) { for (int i = 0; i < row; ++i) { if (col == queenCol[i] || abs(row - i) == abs(col - queenCol[i])) return false; } return true; }}; |
到此這篇關(guān)于C++實(shí)現(xiàn)LeetCode(51.N皇后問題)的文章就介紹到這了,更多相關(guān)C++實(shí)現(xiàn)N皇后問題內(nèi)容請搜索服務(wù)器之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持服務(wù)器之家!
原文鏈接:https://www.cnblogs.com/grandyang/p/4377782.html