本文實(shí)例講述了Python根據(jù)已知鄰接矩陣繪制無向圖操作。分享給大家供大家參考,具體如下:
有六個(gè)點(diǎn):[0,1,2,3,4,5,6],六個(gè)點(diǎn)之間的鄰接矩陣如表格所示,根據(jù)鄰接矩陣?yán)L制出相對(duì)應(yīng)的圖
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
2 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
3 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
5 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
6 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
將點(diǎn)之間的聯(lián)系構(gòu)造成如下矩陣
N = [[0, 3, 5, 1],
[1, 5, 4, 3],
[2, 1, 3, 5],
[3, 5, 1, 4],
[4, 5, 1, 3],
[5, 3, 4, 1],
[6, 3, 1, 4]]
代碼如下
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
# -*- coding:utf-8 -*-#! python3import networkx as nximport matplotlib.pyplot as pltG=nx.Graph()point=[0,1,2,3,4,5,6]G.add_nodes_from(point)edglist=[]N = [[0, 3, 5, 1],[1, 5, 4, 3],[2, 1, 3, 5],[3, 5, 1, 4],[4, 5, 1, 3],[5, 3, 4, 1],[6, 3, 1, 4]]for i in range(7): for j in range(1,4): edglist.append((N[i][0],N[i][j]))G=nx.Graph(edglist)position = nx.circular_layout(G)nx.draw_networkx_nodes(G,position, nodelist=point, node_color="r")nx.draw_networkx_edges(G,position)nx.draw_networkx_labels(G,position)plt.show() |
顯示結(jié)果:
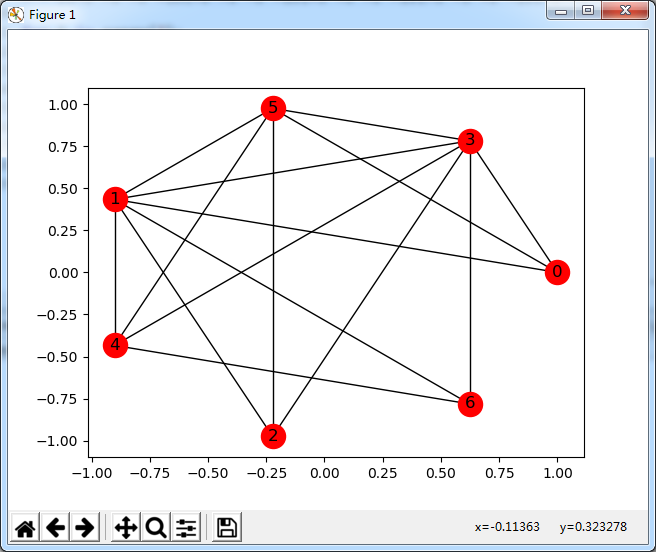
希望本文所述對(duì)大家Python程序設(shè)計(jì)有所幫助。
原文鏈接:https://blog.csdn.net/weixin_40198632/article/details/78418714










