本文實例講述了Python基于更相減損術實現求解最大公約數的方法。分享給大家供大家參考,具體如下:
先從網上摘錄一段算法的描述如下:
更相減損法:也叫 更相減損術,是出自《 九章算術》的一種求最大公約數的算法,它原本是為 約分而設計的,但它適用于任何需要求最大公約數的場合。
《九章算術》是中國古代的數學專著,其中的“更相減損術”可以用來求兩個數的最大公約數,即“可半者半之,不可半者,副置分母、子之數,以少減多,更相減損,求其等也。以等數約之。”
翻譯成現代語言如下:
第一步:任意給定兩個正整數;判斷它們是否都是偶數。若是,則用2約簡;若不是則執行第二步。
第二步:以較大的數減較小的數,接著把所得的差與較小的數比較,并以大數減小數。繼續這個操作,直到所得的減數和差相等為止。
看完上面的描述,我的第一反應是這個描述是不是有問題?從普適性來說的話,應該是有問題的。舉例來說,如果我求解4和4的最大公約數,可半者半之之后,結果肯定錯了!后面的算法也不能夠進行!
不管怎么說,先實現一下上面的算法描述:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# -*- coding:utf-8 -*-#! python2def MaxCommDivisor(m,n): # even process while m % 2 == 0 and n % 2 == 0: m = m / 2 n = n / 2 # exchange order when needed if m < n: m,n = n,m # calculate the max comm divisor while m - n != n: diff = m - n if diff > n: m = diff else: m = n n = diff return nprint(MaxCommDivisor(55,120))print(MaxCommDivisor(55,77))print(MaxCommDivisor(32,64))print(MaxCommDivisor(16,128)) |
運行結果:
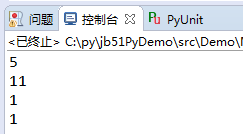
不用說,上面程序執行錯誤百出。那么該如何更正呢?
首先,除的2最終都應該再算回去!這樣,程序修改如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
def MaxCommDivisor(m,n): com_factor = 1 if m == n: return n else: # process for even number while m % 2 == 0 and n % 2 == 0: m = int(m / 2) n = int(n / 2) com_factor *= 2 if m < n: m,n = n,m diff = m - n while n != diff: m = diff if m < n: m,n = n,m diff = m - n return n * com_factorprint(MaxCommDivisor(55,120))print(MaxCommDivisor(55,77))print(MaxCommDivisor(32,64))print(MaxCommDivisor(16,128)) |
通過修改,上面程序執行結果如下
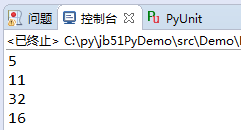
雖說這段程序寫出來看著有點怪怪的,但是總體的算法還是實現了。與輾轉相除等算法相比,這個在循環的層級上有一定的概率會減小。特別是最后的兩組測試數字對兒,這種情況下的效果要好一些。但是,總體上的算法的效率,現在我還不能夠給個準確的衡量。
希望本文所述對大家Python程序設計有所幫助。
原文鏈接:https://blog.csdn.net/grey_csdn/article/details/77416172










