上節(jié)基本完成了SVM的理論推倒，尋找最大化間隔的目標(biāo)最終轉(zhuǎn)換成求解拉格朗日乘子變量alpha的求解問(wèn)題，求出了alpha即可求解出SVM的權(quán)重W，有了權(quán)重也就有了最大間隔距離，但是其實(shí)上節(jié)我們有個(gè)假設(shè)：就是訓(xùn)練集是線(xiàn)性可分的，這樣求出的alpha在[0,infinite]。但是如果數(shù)據(jù)不是線(xiàn)性可分的呢？此時(shí)我們就要允許部分的樣本可以越過(guò)分類(lèi)器，這樣優(yōu)化的目標(biāo)函數(shù)就可以不變，只要引入松弛變量
即可，它表示錯(cuò)分類(lèi)樣本點(diǎn)的代價(jià)，分類(lèi)正確時(shí)它等于0，當(dāng)分類(lèi)錯(cuò)誤時(shí)
，其中Tn表示樣本的真實(shí)標(biāo)簽-1或者1，回顧上節(jié)中，我們把支持向量到分類(lèi)器的距離固定為1，因此兩類(lèi)的支持向量間的距離肯定大于1的，當(dāng)分類(lèi)錯(cuò)誤時(shí)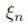
肯定也大于1，如（圖五）所示（這里公式和圖標(biāo)序號(hào)都接上一節(jié)）。
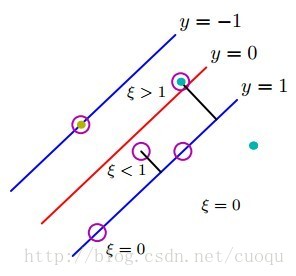
（圖五）
這樣有了錯(cuò)分類(lèi)的代價(jià)，我們把上節(jié)（公式四）的目標(biāo)函數(shù)上添加上這一項(xiàng)錯(cuò)分類(lèi)代價(jià)，得到如（公式八）的形式：
（公式八）
重復(fù)上節(jié)的拉格朗日乘子法步驟，得到（公式九）：
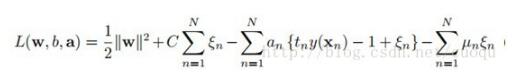
（公式九）
多了一個(gè)Un乘子，當(dāng)然我們的工作就是繼續(xù)求解此目標(biāo)函數(shù)，繼續(xù)重復(fù)上節(jié)的步驟，求導(dǎo)得到（公式十）：
（公式十）
又因?yàn)閍lpha大于0，而且Un大于0，所以0<alpha<C,為了解釋的清晰一些，我們把（公式九）的KKT條件也發(fā)出來(lái)（上節(jié)中的第三類(lèi)優(yōu)化問(wèn)題），注意Un是大于等于0：
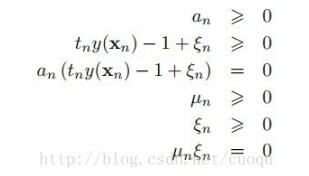
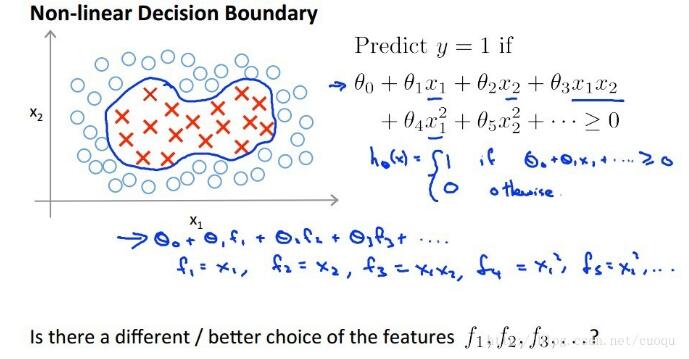
推導(dǎo)到現(xiàn)在，優(yōu)化函數(shù)的形式基本沒(méi)變，只是多了一項(xiàng)錯(cuò)分類(lèi)的價(jià)值，但是多了一個(gè)條件，0<alpha<C，C是一個(gè)常數(shù)，它的作用就是在允許有錯(cuò)誤分類(lèi)的情況下，控制最大化間距，它太大了會(huì)導(dǎo)致過(guò)擬合，太小了會(huì)導(dǎo)致欠擬合。接下來(lái)的步驟貌似大家都應(yīng)該知道了，多了一個(gè)C常量的限制條件，然后繼續(xù)用SMO算法優(yōu)化求解二次規(guī)劃，但是我想繼續(xù)把核函數(shù)也一次說(shuō)了，如果樣本線(xiàn)性不可分，引入核函數(shù)后，把樣本映射到高維空間就可以線(xiàn)性可分，如（圖六）所示的線(xiàn)性不可分的樣本：
（圖六）
在（圖六）中，現(xiàn)有的樣本是很明顯線(xiàn)性不可分，但是加入我們利用現(xiàn)有的樣本X之間作些不同的運(yùn)算，如（圖六）右邊所示的樣子，而讓f作為新的樣本（或者說(shuō)新的特征）是不是更好些？現(xiàn)在把X已經(jīng)投射到高維度上去了，但是f我們不知道，此時(shí)核函數(shù)就該上場(chǎng)了，以高斯核函數(shù)為例，在（圖七）中選幾個(gè)樣本點(diǎn)作為基準(zhǔn)點(diǎn)，來(lái)利用核函數(shù)計(jì)算f,如（圖七）所示：
（圖七）
這樣就有了f,而核函數(shù)此時(shí)相當(dāng)于對(duì)樣本的X和基準(zhǔn)點(diǎn)一個(gè)度量，做權(quán)重衰減，形成依賴(lài)于x的新的特征f,把f放在上面說(shuō)的SVM中繼續(xù)求解alpha，然后得出權(quán)重就行了，原理很簡(jiǎn)單吧，為了顯得有點(diǎn)學(xué)術(shù)味道，把核函數(shù)也做個(gè)樣子加入目標(biāo)函數(shù)中去吧，如（公式十一）所示：
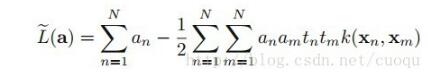
（公式十一）
其中K(Xn,Xm)是核函數(shù)，和上面目標(biāo)函數(shù)比沒(méi)有多大的變化，用SMO優(yōu)化求解就行了，代碼如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
def smoPK(dataMatIn, classLabels, C, toler, maxIter): #full Platt SMO oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler) iter = 0 entireSet = True; alphaPairsChanged = 0 while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): alphaPairsChanged = 0 if entireSet: #go over all for i in range(oS.m): alphaPairsChanged += innerL(i,oS) print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) iter += 1 else:#go over non-bound (railed) alphas nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] for i in nonBoundIs: alphaPairsChanged += innerL(i,oS) print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) iter += 1 if entireSet: entireSet = False #toggle entire set loop elif (alphaPairsChanged == 0): entireSet = True print "iteration number: %d" % iter return oS.b,oS.alphas |
下面演示一個(gè)小例子，手寫(xiě)識(shí)別。
(1)收集數(shù)據(jù)：提供文本文件
(2)準(zhǔn)備數(shù)據(jù)：基于二值圖像構(gòu)造向量
(3)分析數(shù)據(jù)：對(duì)圖像向量進(jìn)行目測(cè)
(4)訓(xùn)練算法：采用兩種不同的核函數(shù)，并對(duì)徑向基函數(shù)采用不同的設(shè)置來(lái)運(yùn)行SMO算法。
(5)測(cè)試算法：編寫(xiě)一個(gè)函數(shù)來(lái)測(cè)試不同的核函數(shù)，并計(jì)算錯(cuò)誤率
(6)使用算法：一個(gè)圖像識(shí)別的完整應(yīng)用還需要一些圖像處理的只是，此demo略。
完整代碼如下：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
|
from numpy import *from time import sleep def loadDataSet(fileName): dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr = line.strip().split('\t') dataMat.append([float(lineArr[0]), float(lineArr[1])]) labelMat.append(float(lineArr[2])) return dataMat,labelMat def selectJrand(i,m): j=i #we want to select any J not equal to i while (j==i): j = int(random.uniform(0,m)) return j def clipAlpha(aj,H,L): if aj > H: aj = H if L > aj: aj = L return aj def smoSimple(dataMatIn, classLabels, C, toler, maxIter): dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose() b = 0; m,n = shape(dataMatrix) alphas = mat(zeros((m,1))) iter = 0 while (iter < maxIter): alphaPairsChanged = 0 for i in range(m): fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)): j = selectJrand(i,m) fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b Ej = fXj - float(labelMat[j]) alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy(); if (labelMat[i] != labelMat[j]): L = max(0, alphas[j] - alphas[i]) H = min(C, C + alphas[j] - alphas[i]) else: L = max(0, alphas[j] + alphas[i] - C) H = min(C, alphas[j] + alphas[i]) if L==H: print "L==H"; continue eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T if eta >= 0: print "eta>=0"; continue alphas[j] -= labelMat[j]*(Ei - Ej)/eta alphas[j] = clipAlpha(alphas[j],H,L) if (abs(alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; continue alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j #the update is in the oppostie direction b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T if (0 < alphas[i]) and (C > alphas[i]): b = b1 elif (0 < alphas[j]) and (C > alphas[j]): b = b2 else: b = (b1 + b2)/2.0 alphaPairsChanged += 1 print "iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) if (alphaPairsChanged == 0): iter += 1 else: iter = 0 print "iteration number: %d" % iter return b,alphas def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space m,n = shape(X) K = mat(zeros((m,1))) if kTup[0]=='lin': K = X * A.T #linear kernel elif kTup[0]=='rbf': for j in range(m): deltaRow = X[j,:] - A K[j] = deltaRow*deltaRow.T K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab else: raise NameError('Houston We Have a Problem -- \ That Kernel is not recognized') return K class optStruct: def __init__(self,dataMatIn, classLabels, C, toler, kTup): # Initialize the structure with the parameters self.X = dataMatIn self.labelMat = classLabels self.C = C self.tol = toler self.m = shape(dataMatIn)[0] self.alphas = mat(zeros((self.m,1))) self.b = 0 self.eCache = mat(zeros((self.m,2))) #first column is valid flag self.K = mat(zeros((self.m,self.m))) for i in range(self.m): self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup) def calcEk(oS, k): fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b) Ek = fXk - float(oS.labelMat[k]) return Ek def selectJ(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej maxK = -1; maxDeltaE = 0; Ej = 0 oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E validEcacheList = nonzero(oS.eCache[:,0].A)[0] if (len(validEcacheList)) > 1: for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E if k == i: continue #don't calc for i, waste of time Ek = calcEk(oS, k) deltaE = abs(Ei - Ek) if (deltaE > maxDeltaE): maxK = k; maxDeltaE = deltaE; Ej = Ek return maxK, Ej else: #in this case (first time around) we don't have any valid eCache values j = selectJrand(i, oS.m) Ej = calcEk(oS, j) return j, Ej def updateEk(oS, k):#after any alpha has changed update the new value in the cache Ek = calcEk(oS, k) oS.eCache[k] = [1,Ek] def innerL(i, oS): Ei = calcEk(oS, i) if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)): j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy(); if (oS.labelMat[i] != oS.labelMat[j]): L = max(0, oS.alphas[j] - oS.alphas[i]) H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) else: L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C) H = min(oS.C, oS.alphas[j] + oS.alphas[i]) if L==H: print "L==H"; return 0 eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel if eta >= 0: print "eta>=0"; return 0 oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta oS.alphas[j] = clipAlpha(oS.alphas[j],H,L) updateEk(oS, j) #added this for the Ecache if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0 oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j] b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j] if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1 elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2 else: oS.b = (b1 + b2)/2.0 return 1 else: return 0 def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #full Platt SMO oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup) iter = 0 entireSet = True; alphaPairsChanged = 0 while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): alphaPairsChanged = 0 if entireSet: #go over all for i in range(oS.m): alphaPairsChanged += innerL(i,oS) print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) iter += 1 else:#go over non-bound (railed) alphas nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] for i in nonBoundIs: alphaPairsChanged += innerL(i,oS) print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) iter += 1 if entireSet: entireSet = False #toggle entire set loop elif (alphaPairsChanged == 0): entireSet = True print "iteration number: %d" % iter return oS.b,oS.alphas def calcWs(alphas,dataArr,classLabels): X = mat(dataArr); labelMat = mat(classLabels).transpose() m,n = shape(X) w = zeros((n,1)) for i in range(m): w += multiply(alphas[i]*labelMat[i],X[i,:].T) return w def testRbf(k1=1.3): dataArr,labelArr = loadDataSet('testSetRBF.txt') b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important datMat=mat(dataArr); labelMat = mat(labelArr).transpose() svInd=nonzero(alphas.A>0)[0] sVs=datMat[svInd] #get matrix of only support vectors labelSV = labelMat[svInd]; print "there are %d Support Vectors" % shape(sVs)[0] m,n = shape(datMat) errorCount = 0 for i in range(m): kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1)) predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b if sign(predict)!=sign(labelArr[i]): errorCount += 1 print "the training error rate is: %f" % (float(errorCount)/m) dataArr,labelArr = loadDataSet('testSetRBF2.txt') errorCount = 0 datMat=mat(dataArr); labelMat = mat(labelArr).transpose() m,n = shape(datMat) for i in range(m): kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1)) predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b if sign(predict)!=sign(labelArr[i]): errorCount += 1 print "the test error rate is: %f" % (float(errorCount)/m) def img2vector(filename): returnVect = zeros((1,1024)) fr = open(filename) for i in range(32): lineStr = fr.readline() for j in range(32): returnVect[0,32*i+j] = int(lineStr[j]) return returnVect def loadImages(dirName): from os import listdir hwLabels = [] trainingFileList = listdir(dirName) #load the training set m = len(trainingFileList) trainingMat = zeros((m,1024)) for i in range(m): fileNameStr = trainingFileList[i] fileStr = fileNameStr.split('.')[0] #take off .txt classNumStr = int(fileStr.split('_')[0]) if classNumStr == 9: hwLabels.append(-1) else: hwLabels.append(1) trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr)) return trainingMat, hwLabels def testDigits(kTup=('rbf', 10)): dataArr,labelArr = loadImages('trainingDigits') b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup) datMat=mat(dataArr); labelMat = mat(labelArr).transpose() svInd=nonzero(alphas.A>0)[0] sVs=datMat[svInd] labelSV = labelMat[svInd]; print "there are %d Support Vectors" % shape(sVs)[0] m,n = shape(datMat) errorCount = 0 for i in range(m): kernelEval = kernelTrans(sVs,datMat[i,:],kTup) predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b if sign(predict)!=sign(labelArr[i]): errorCount += 1 print "the training error rate is: %f" % (float(errorCount)/m) dataArr,labelArr = loadImages('testDigits') errorCount = 0 datMat=mat(dataArr); labelMat = mat(labelArr).transpose() m,n = shape(datMat) for i in range(m): kernelEval = kernelTrans(sVs,datMat[i,:],kTup) predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b if sign(predict)!=sign(labelArr[i]): errorCount += 1 print "the test error rate is: %f" % (float(errorCount)/m) '''''#######******************************** Non-Kernel VErsions below '''#######******************************** class optStructK: def __init__(self,dataMatIn, classLabels, C, toler): # Initialize the structure with the parameters self.X = dataMatIn self.labelMat = classLabels self.C = C self.tol = toler self.m = shape(dataMatIn)[0] self.alphas = mat(zeros((self.m,1))) self.b = 0 self.eCache = mat(zeros((self.m,2))) #first column is valid flag def calcEkK(oS, k): fXk = float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b Ek = fXk - float(oS.labelMat[k]) return Ek def selectJK(i, oS, Ei): #this is the second choice -heurstic, and calcs Ej maxK = -1; maxDeltaE = 0; Ej = 0 oS.eCache[i] = [1,Ei] #set valid #choose the alpha that gives the maximum delta E validEcacheList = nonzero(oS.eCache[:,0].A)[0] if (len(validEcacheList)) > 1: for k in validEcacheList: #loop through valid Ecache values and find the one that maximizes delta E if k == i: continue #don't calc for i, waste of time Ek = calcEk(oS, k) deltaE = abs(Ei - Ek) if (deltaE > maxDeltaE): maxK = k; maxDeltaE = deltaE; Ej = Ek return maxK, Ej else: #in this case (first time around) we don't have any valid eCache values j = selectJrand(i, oS.m) Ej = calcEk(oS, j) return j, Ej def updateEkK(oS, k):#after any alpha has changed update the new value in the cache Ek = calcEk(oS, k) oS.eCache[k] = [1,Ek] def innerLK(i, oS): Ei = calcEk(oS, i) if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)): j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy(); if (oS.labelMat[i] != oS.labelMat[j]): L = max(0, oS.alphas[j] - oS.alphas[i]) H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) else: L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C) H = min(oS.C, oS.alphas[j] + oS.alphas[i]) if L==H: print "L==H"; return 0 eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T if eta >= 0: print "eta>=0"; return 0 oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta oS.alphas[j] = clipAlpha(oS.alphas[j],H,L) updateEk(oS, j) #added this for the Ecache if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0 oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1 elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2 else: oS.b = (b1 + b2)/2.0 return 1 else: return 0 def smoPK(dataMatIn, classLabels, C, toler, maxIter): #full Platt SMO oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler) iter = 0 entireSet = True; alphaPairsChanged = 0 while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): alphaPairsChanged = 0 if entireSet: #go over all for i in range(oS.m): alphaPairsChanged += innerL(i,oS) print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) iter += 1 else:#go over non-bound (railed) alphas nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] for i in nonBoundIs: alphaPairsChanged += innerL(i,oS) print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged) iter += 1 if entireSet: entireSet = False #toggle entire set loop elif (alphaPairsChanged == 0): entireSet = True print "iteration number: %d" % iter return oS.b,oS.alphas |
運(yùn)行結(jié)果如（圖八）所示：
（圖八）
上面代碼有興趣的可以讀讀，用的話(huà)，建議使用libsvm。
參考文獻(xiàn)：
[1]machine learning in action. PeterHarrington
[2] pattern recognition and machinelearning. Christopher M. Bishop
[3]machine learning.Andrew Ng
以上就是本文的全部?jī)?nèi)容，希望對(duì)大家的學(xué)習(xí)有所幫助，也希望大家多多支持服務(wù)器之家。
原文鏈接：http://blog.csdn.net/marvin521/article/details/9305497
