
交并比(Intersection-over-Union,IoU),目標(biāo)檢測(cè)中使用的一個(gè)概念,我們?cè)谶M(jìn)行目標(biāo)檢測(cè)算法測(cè)試時(shí),重要的指標(biāo),是產(chǎn)生的預(yù)測(cè)框(candidate bound)與標(biāo)記框(ground truth bound)的交疊率,即它們的交集與并集的比值。最理想情況是完全重疊,即比值為1。
通常,我們所說(shuō)的目標(biāo)檢測(cè)檢測(cè)的框是規(guī)則的矩形框,計(jì)算IOU也非常簡(jiǎn)單,一般兩種方法:
- 兩個(gè)矩形的寬之和減去組合后的矩形的寬就是重疊矩形的寬,同比重疊矩形的高。
- 右下角的最小值減去左上角的最大值就是重疊矩形的寬,同比高。
上述規(guī)則四邊形(矩形)IOU計(jì)算方式一的 Python實(shí)現(xiàn)
def calculate_regular_iou(rec1, rec2):
"""
computing IoU
:param rec1: (y0, x0, y1, x1), which reflects
(top, left, bottom, right)
:param rec2: (y0, x0, y1, x1)
:return: scala value of IoU
"""
S_rec1 = (rec1[2] - rec1[0]) * (rec1[3] - rec1[1])
S_rec2 = (rec2[2] - rec2[0]) * (rec2[3] - rec2[1])
sum_area = S_rec1 + S_rec2
?
left_line = max(rec1[1], rec2[1])
right_line = min(rec1[3], rec2[3])
top_line = max(rec1[0], rec2[0])
bottom_line = min(rec1[2], rec2[2])
?
if left_line >= right_line or top_line >= bottom_line:
return 0
else:
intersect = (right_line - left_line) * (bottom_line - top_line)
return (intersect / (sum_area - intersect)) * 1.0
if __name__ == '__main__':
# (top, left, bottom, right)
rect1 = [551, 26, 657, 45]
rect2 = [552, 27, 672, 46]
iou = calculate_regular_iou(rect1, rect2)
上述規(guī)則四邊形(矩形)IOU計(jì)算方式二的 Python 實(shí)現(xiàn)
def compute_regular_iou_other(rec1, rec2):
"""
computing IoU
:param rec1: (y0, x0, y1, x1), which reflects
(top, left, bottom, right)
:param rec2: (y0, x0, y1, x1)
:return: scala value of IoU
"""
areas1 = (rec1[3] - rec1[1]) * (rec1[2] - rec1[0])
areas2 = (rec2[3] - rec2[1]) * (rec2[2] - rec2[0])
?
left = max(rec1[1],rec2[1])
?
right = min(rec1[3],rec2[3])
?
top = max(rec1[0], rec2[0])
?
bottom = min(rec1[2], rec2[2])
?
w = max(0, right - left)
h = max(0, bottom - top)
?
return w*h / (areas2 + areas1 - w*h)
?
if __name__ == '__main__':
# (top, left, bottom, right)
rect1 = [551, 26, 657, 45]
rect2 = [552, 27, 672, 46]
iou = compute_regular_iou_other(rect1, rect2)
但是,對(duì)于不規(guī)則四邊形就不能通過(guò)上述這兩種方式來(lái)計(jì)算,這里可以使用Python的 Shapely 庫(kù)實(shí)現(xiàn),Python 實(shí)現(xiàn)如下:
import numpy as np
import shapely
from shapely.errors import TopologicalError
from shapely.geometry import Polygon,MultiPoint
?
def to_polygon(quadrilateral):
"""
?
:param quadrilateral: 四邊形四個(gè)點(diǎn)坐標(biāo)的一維數(shù)組表示,[x,y,x,y....]
:return: 四邊形二維數(shù)組, Polygon四邊形對(duì)象
"""
# 四邊形二維數(shù)組表示
quadrilateral_array = np.array(quadrilateral).reshape(4, 2)
# Polygon四邊形對(duì)象,會(huì)自動(dòng)計(jì)算四個(gè)點(diǎn),最后四個(gè)點(diǎn)順序?yàn)椋鹤笊?nbsp;左下 右下 右上 左上
quadrilateral_polygon = Polygon(quadrilateral_array).convex_hull
?
return quadrilateral_array, quadrilateral_polygon
?
def calculate_iou(actual_quadrilateral, predict_quadrilateral):
"""
?
:param actual_quadrilateral: 預(yù)測(cè)四邊形四個(gè)點(diǎn)坐標(biāo)的一維數(shù)組表示,[x,y,x,y....]
:param predict_quadrilateral: 期望四邊形四個(gè)點(diǎn)坐標(biāo)的一維數(shù)組表示,[x,y,x,y....]
:return:
"""
# 預(yù)測(cè)四邊形二維數(shù)組, 預(yù)測(cè)四邊形 Polygon 對(duì)象
actual_quadrilateral_array, actual_quadrilateral_polygon = to_polygon(actual_quadrilateral)
# 期望四邊形二維數(shù)組, 期望四邊形 Polygon 對(duì)象
predict_quadrilateral_array, predict_quadrilateral_polygon = to_polygon(predict_quadrilateral)
?
# 合并兩個(gè)box坐標(biāo),變?yōu)?*2 便于后面計(jì)算并集面積
union_poly = np.concatenate((actual_quadrilateral_array, predict_quadrilateral_array))
# 兩兩四邊形是否存在交集
inter_status = actual_quadrilateral_polygon.intersects(predict_quadrilateral_polygon)
# 如果兩四邊形相交,則進(jìn)iou計(jì)算
if inter_status:
try:
# 交集面積
inter_area = actual_quadrilateral_polygon.intersection(predict_quadrilateral_polygon).area
# 并集面積 計(jì)算方式一
#union_area = poly1.area + poly2.area - inter_area
# 并集面積 計(jì)算方式二
union_area = MultiPoint(union_poly).convex_hull.area
# 若并集面積等于0,則iou = 0
if union_area == 0:
iou = 0
else:
# 第一種計(jì)算的是: 交集部分/包含兩個(gè)四邊形最小多邊形的面積
iou = float(inter_area) / union_area
# 第二種: 交集 / 并集(常見(jiàn)矩形框IOU計(jì)算方式)
# iou=float(inter_area) /(poly1.area+poly2.area-inter_area)
except shapely.errors.TopologicalError :
print('shapely.errors.TopologicalError occured, iou set to 0')
iou = 0
else:
iou = 0
?
return iou
?
if __name__ == '__main__':
actual_quadrilateral = [908, 215, 934, 312, 752, 355, 728, 252]
predict_quadrilateral = [923, 308, 758, 342, 741, 262, 907, 228]
iou = calculate_iou(actual_quadrilateral, predict_quadrilateral)
print(iou)
避坑指南
運(yùn)行代碼拋出 WinError 126 錯(cuò)誤
在使用Python中的使用 import shapely 時(shí)不會(huì)報(bào)錯(cuò),但是在使用 from shapely.geometry import Polygon,MultiPoint 會(huì)報(bào)錯(cuò),報(bào)錯(cuò)的詳細(xì)信息如下圖:

報(bào)錯(cuò)的主要原因就出現(xiàn)在 geos_c.dll 這里,看了網(wǎng)上很多文章大部分說(shuō)是由于 geos_c.dll 文件缺失導(dǎo)致報(bào)錯(cuò)。嘗試在網(wǎng)上找了幾個(gè) geos_c.dll 文件放到 C:\Windows\System32 下仍然沒(méi)有解決問(wèn)題。
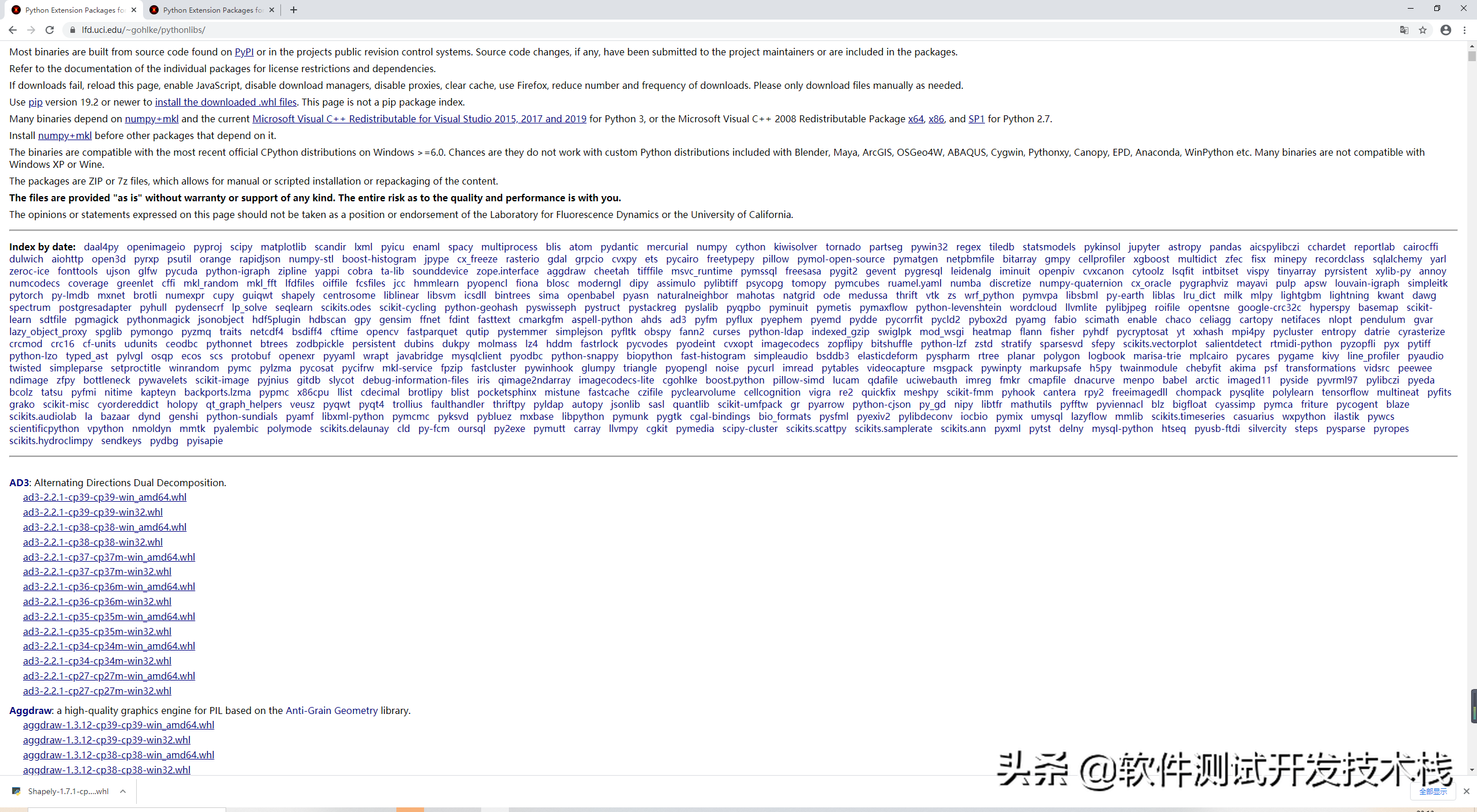
最終解決方案:通過(guò) pip uninstall Shapely 卸載原來(lái)安裝的 Shapely 然后 在 https://www.lfd.uci.edu/~gohlke/pythonlibs/#shapely,如上圖,這里下載對(duì)應(yīng)版本的whl文件安裝,安裝這個(gè)whl 就可以解決該問(wèn)題。
whl文件下載404錯(cuò)誤
在 https://www.lfd.uci.edu/~gohlke/pythonlibs/#shapely 下載制定版本的whl時(shí),出現(xiàn)404錯(cuò)誤。如下。

此時(shí)改用 chrome 瀏覽器重新嘗試下載,即可解決。










