題目:在數組中的兩個數字如果前面一個數字大于后面的數字,則這兩個數字組成一個逆序對。輸入一個數組,求出這個數組中的逆序對的總數
例如在數組{7,5,6,4}中,一共存在5對逆序對,分別是{7,6},{7,5},{7,4},{6,4},{5,4}。
看到這個題目,我們的第一反應就是順序掃描整個數組。每掃描到一個數組的時候,逐個比較該數字和它后面的數字的大小。如果后面的數字比它小,則這兩個數字就組成一個逆序對。假設數組中含有n個數字。由于每個數字都要和o(n)個數字做比較,因此這個算法的時間復雜度為o(n2)。我們嘗試找找更快的算法。
我們以數組{7,5,6,4}為例來分析統計逆序對的過程,每次掃描到一個數字的時候,我們不能拿它和后面的每一個數字做比較,否則時間復雜度就是o(n2)因此我們可以考慮先比較兩個相鄰的數字。
如下圖所示,我們先把數組分解稱兩個長度為2的子數組,再把這兩個子數組分別茶城兩個長度為1的子數組。接下來一邊合并相鄰的子數組,一邊統計逆序對的數目。在第一對長度為1的子數組{7},{5}中7大于5,因此{7,5}組成一個逆序對。同樣在第二對長度為1的子數組{6},{4}中也有逆序對{6,4}。由于我們已經統計了這兩隊子數組內部逆序對,因此需要把這兩對子數組排序,以免在以后的統計過程中再重復統計。
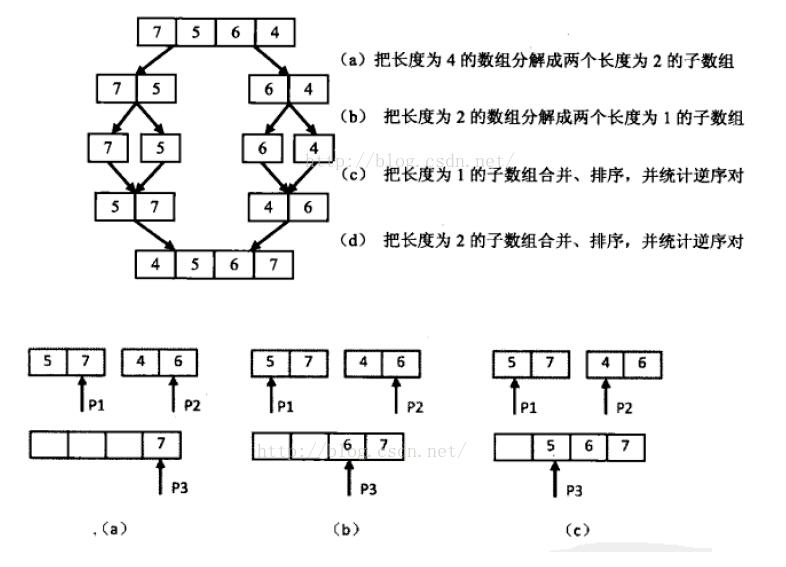
接下來我們統計兩個長度為2的子數組之間的逆序對。
我們先用兩個指針分別指向兩個子數組的末尾,并每次比較兩個指針指向的數字。如果第一個子數組中的數字大于第二個子數組中的數字,則構成逆序對,并且逆序對的數目等于第二個子數組中的剩余數字的個數。如果第一個數組中的數字小于或等于第二個數組中的數字,則不構成逆序對。每一次比較的時候,我們都把較大的數字從后往前復制到一個輔助數組中去,確保輔助數組中的數字是遞增排序的。在把較大的數字復制到數組之后,把對應的指針向前移動一位,接著來進行下一輪的比較。
經過前面詳細的討論,我們可以總結出統計逆序對的過程:先把數組分隔成子數組,先統計出子數組內部的逆序對的數目,然后再統計出兩個相鄰子數組之間的逆序對的數目。在統計逆序對的過程中,還需要對數組進行排序。如果對排序算法很熟悉,我們不難發現這個排序的過程就是歸并排序。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
static int count = 0; // 將有二個有序數列a[first...mid]和a[mid...last]合并。 static void mergearray(int a[], int first, int mid, int last, int temp[]) { int i = first, j = mid + 1; int m = mid, n = last; int k = 0; while (i <= m && j <= n) { if (a[i] > a[j]) { // 左數組比右數組大 temp[k++] = a[j++]; // 因為如果a[i]此時比右數組的當前元素a[j]大, // 那么左數組中a[i]后面的元素就都比a[j]大 // 【因為數組此時是有序數組】 count += mid - i + 1; } else { temp[k++] = a[i++]; } } while (i <= m) { temp[k++] = a[i++]; } while (j <= n) { temp[k++] = a[j++]; } for (i = 0; i < k; i++) a[first + i] = temp[i]; } static void mergesort(int a[], int first, int last, int temp[]) { if (first < last) { int mid = (first + last) / 2; mergesort(a, first, mid, temp); // 左邊有序 mergesort(a, mid + 1, last, temp); // 右邊有序 mergearray(a, first, mid, last, temp); // 再將二個有序數列合并 } } static void mergesort(int a[]) { int[] p = new int[a.length]; mergesort(a, 0, a.length - 1, p); } |
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:https://blog.csdn.net/abc7845129630/article/details/52740746