二叉樹(shù)在計(jì)算機(jī)中的存儲(chǔ)方式往往線性結(jié)構(gòu),線性存儲(chǔ)分為順序存儲(chǔ)和鏈?zhǔn)酱鎯?chǔ),將二叉樹(shù)按層序編號(hào)。
順序結(jié)構(gòu):按編號(hào)的順序進(jìn)行存儲(chǔ),對(duì)于完全二叉樹(shù)而言,順序存儲(chǔ)可以反映二叉樹(shù)的邏輯,但是對(duì)于大多數(shù)的二叉樹(shù)則無(wú)法反映其邏輯關(guān)系,不過(guò)可以用 ^ 來(lái)代替不存在的結(jié)點(diǎn),但是如果這個(gè)樹(shù)是一個(gè)右斜樹(shù),就非常浪費(fèi)存儲(chǔ)空間。所以二叉樹(shù)的存儲(chǔ)形式一般為鏈?zhǔn)酱鎯?chǔ)結(jié)構(gòu)。
鏈?zhǔn)酱鎯?chǔ):每一個(gè)結(jié)點(diǎn)都分有一個(gè)數(shù)據(jù)域(data)和兩個(gè)指針域(lchild和rchild),指針域分別指向左孩子和右孩子,若為空則為null。遍歷方式有四種:前序遍歷、中序遍歷、后序遍歷及層序遍歷,前三種遍歷方式采用遞歸的思想進(jìn)行遍歷。
為方便理解,畫(huà)一個(gè)樹(shù)并結(jié)合代碼
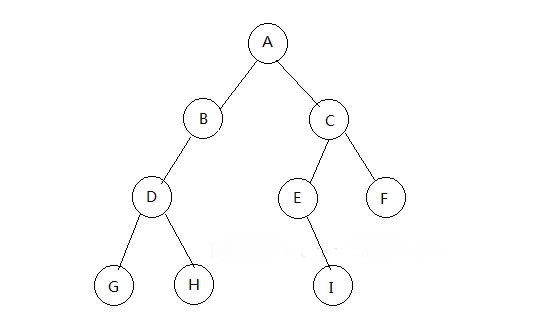
前序遍歷:若二叉樹(shù)為空則返回null,否則先訪問(wèn)根節(jié)點(diǎn)然后遍歷左子樹(shù),再遍歷右子樹(shù),如圖:abdghceif
代碼如下:
|
1
2
3
4
5
6
7
|
void preordertraverse(bitree t) { if(t == null) /*為空返回*/ return; printf("%c",t->data); /*輸出該結(jié)點(diǎn)的信息*/ preordertraverse(t->lchild); /*遍歷左子樹(shù)*/ preordertraverse(t->rchild); /*遍歷右子樹(shù)*/} |
中序遍歷:若二叉樹(shù)為空則返回null,否則從根節(jié)點(diǎn)出發(fā)訪問(wèn)左子樹(shù),然后訪問(wèn)根結(jié)點(diǎn),最后訪問(wèn)右子樹(shù),如圖:gdhbaeicf
代碼如下:
|
1
2
3
4
5
6
7
|
void inordertraverse(bitree t) { if(t == null) /*為空返回*/ return; inordertraverse(t->lchild); /*遍歷左子樹(shù)*/ printf("%c",t->data); /*輸出該結(jié)點(diǎn)的信息*/ inordertraverse(t->rchild); /*遍歷右子樹(shù)*/} |
后序遍歷:若二叉樹(shù)為空則返回null,否則以先葉子后結(jié)點(diǎn)的方式進(jìn)行訪問(wèn)最后到根結(jié)點(diǎn)遍歷結(jié)束,如圖:ghdbiefca
代碼如下:
|
1
2
3
4
5
6
7
|
void postordertraverse(bitree t) { if(t == null) /*為空返回*/ return; postordertraverse(t->lchild); /*遍歷左子樹(shù)*/ postordertraverse(t->rchild); /*遍歷右子樹(shù)*/ printf("%c",t->data); /*輸出該結(jié)點(diǎn)的信息*/} |
層序遍歷:若二叉樹(shù)為空則返回null,否則從第一層開(kāi)始進(jìn)行訪問(wèn),如圖:abcdefghi,按編號(hào)進(jìn)行輸出或操作即可
總結(jié)
以上就是這篇文章的全部?jī)?nèi)容了,希望本文的內(nèi)容對(duì)大家的學(xué)習(xí)或者工作具有一定的參考學(xué)習(xí)價(jià)值,謝謝大家對(duì)服務(wù)器之家的支持。如果你想了解更多相關(guān)內(nèi)容請(qǐng)查看下面相關(guān)鏈接
原文鏈接:https://blog.csdn.net/sdr_zd/article/details/52214723