選擇排序概念
選擇排序也是一種交換排序算法,和冒泡排序有一定的相似度,因此個人認(rèn)為選擇排序可以視為冒泡排序的一種改進(jìn)算法。它的思路是這樣的:
設(shè)現(xiàn)在要給數(shù)組arr[]排序,它有n個元素。
1對第一個元素(Java中,下標(biāo)為0)和第二個元素進(jìn)行比較,如果前者大于后者,那么它一定不是最小的,但是我們并不像冒泡排序一樣急著交換。我們可以設(shè)置一個臨時變量a,存儲這個目前最小的元素的下標(biāo)。然后我們把這個目前最小的元素繼續(xù)和第三個元素做比較,如果它仍不是最小的,那么,我們再修改a的值。如此直到和最后一個元素比較完,可以肯定a存儲的一定是最小的元素的下標(biāo)。
2.如果a的值不為0(初始值,即第一個元素的下標(biāo)),交換下標(biāo)為a和0的兩個元素。
3.重復(fù)上述過程,這次從下標(biāo)為1的元素開始比較,因為下標(biāo)為0的位置已經(jīng)放好了最小的元素了。
4.如此直到只剩下最后一個元素,可以肯定這個元素就是最大的了。
5.排序完成。
很顯然,這個算法也需要n-1輪排序。
需要注意的是,以上闡述的只是每次找最小值的辦法。實際上也可以每次找最大值,不過那就需要每次放到數(shù)組尾巴上了。
Java實現(xiàn)代碼:
SelectArray.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
package ch02;public class SelectArray { // 數(shù)組 private long[] arr; // 數(shù)組中有效數(shù)據(jù)的大小 private int elems; // 默認(rèn)構(gòu)造函數(shù) public SelectArray() { arr = new long[50]; } public SelectArray(int max) { arr = new long[max]; } // 插入數(shù)據(jù) public void insert(long value) { arr[elems] = value; elems++; } // 顯示數(shù)據(jù) public void display() { for (int i = 0; i < elems; i++) { System.out.print(arr[i] + " "); } System.out.println(); } // 選擇排序 public void selectSort(){ int min = 0; long tmp = 0L; for(int i = 0; i < elems -1; i++){ min = i; for(int j = i + 1; j < elems; j++) { if(arr[j] < arr[min]) { min = j; } } tmp = arr[i]; arr[i] = arr[min]; arr[min] = tmp; } }} |
測試代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
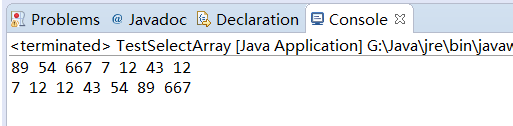
package ch02;public class TestSelectArray { public static void main(String[] args) { SelectArray sArr = new SelectArray(); sArr.insert(89); sArr.insert(54); sArr.insert(667); sArr.insert(7); sArr.insert(12); sArr.insert(43); sArr.insert(12); sArr.display(); sArr.selectSort(); sArr.display(); }} |
結(jié)果: