這份筆記整理了整整一個星期,每一行代碼都是自己默寫完成,并測試運行成功,同時也回顧了一下《劍指offer》這本書中和鏈表有關的講解,希望對筆試和面試有所幫助。
本文包含鏈表的以下內容:
1、單鏈表的創建和遍歷
2、求單鏈表中節點的個數
3、查找單鏈表中的倒數第k個結點(劍指offer,題15)
4、查找單鏈表中的中間結點
5、合并兩個有序的單鏈表,合并之后的鏈表依然有序【出現頻率高】(劍指offer,題17)
6、單鏈表的反轉【出現頻率最高】(劍指offer,題16)
7、從尾到頭打印單鏈表(劍指offer,題5)
8、判斷單鏈表是否有環
9、取出有環鏈表中,環的長度
10、單鏈表中,取出環的起始點(劍指offer,題56)。本題需利用上面的第8題和第9題。
11、判斷兩個單鏈表相交的第一個交點(劍指offer,題37)
1、單鏈表的創建和遍歷:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
public class LinkList {public Node head;public Node current;//方法:向鏈表中添加數據public void add(int data) { //判斷鏈表為空的時候 if (head == null) {//如果頭結點為空,說明這個鏈表還沒有創建,那就把新的結點賦給頭結點 head = new Node(data); current = head; } else { //創建新的結點,放在當前節點的后面(把新的結點合鏈表進行關聯) current.next = new Node(data); //把鏈表的當前索引向后移動一位 current = current.next; //此步操作完成之后,current結點指向新添加的那個結點 }}//方法:遍歷鏈表(打印輸出鏈表。方法的參數表示從節點node開始進行遍歷public void print(Node node) { if (node == null) { return; }current = node; while (current != null) { System.out.println(current.data); current = current.next; }} class Node {//注:此處的兩個成員變量權限不能為private,因為private的權限是僅對本類訪問。 int data; //數據域 Node next;//指針域 public Node(int data) { this.data = data;}}public static void main(String[] args) {LinkList list = new LinkList();//向LinkList中添加數據 for (int i = 0; i < 10; i++) { list.add(i); } list.print(list.head);// 從head節點開始遍歷輸出}} |
上方代碼中,這里面的Node節點采用的是內部類來表示(33行)。使用內部類的最大好處是可以和外部類進行私有操作的互相訪問。
注:內部類訪問的特點是:內部類可以直接訪問外部類的成員,包括私有;外部類要訪問內部類的成員,必須先創建對象。
為了方便添加和遍歷的操作,在LinkList類中添加一個成員變量current,用來表示當前節點的索引(03行)。
這里面的遍歷鏈表的方法(20行)中,參數node表示從node節點開始遍歷,不一定要從head節點遍歷。
2、求單鏈表中節點的個數:
注意檢查鏈表是否為空。時間復雜度為O(n)。這個比較簡單。
核心代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
//方法:獲取單鏈表的長度public int getLength(Node head) { if (head == null) { return 0; } int length = 0; Node current = head; while (current != null) { length++; current = current.next; } return length;} |
3、查找單鏈表中的倒數第k個結點:
3.1 普通思路:
先將整個鏈表從頭到尾遍歷一次,計算出鏈表的長度size,得到鏈表的長度之后,就好辦了,直接輸出第(size-k)個節點就可以了(注意鏈表為空,k為0,k為1,k大于鏈表中節點個數時的情況
)。時間復雜度為O(n),大概思路如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public int findLastNode(int index) { //index代表的是倒數第index的那個結點 //第一次遍歷,得到鏈表的長度size if (head == null) { return -1; } current = head; while (current != null) { size++; current = current.next;} //第二次遍歷,輸出倒數第index個結點的數據 current = head; for (int i = 0; i < size - index; i++) { current = current.next; }return current.data;} |
如果面試官不允許你遍歷鏈表的長度,該怎么做呢?接下來就是。
3.2 改進思路:(這種思路在其他題目中也有應用)
這里需要聲明兩個指針:即兩個結點型的變量first和second,首先讓first和second都指向第一個結點,然后讓second結點往后挪k-1個位置,此時first和second就間隔了k-1個位置,然后整體向后移動這兩個節點,直到second節點走到最后一個結點的時候,此時first節點所指向的位置就是倒數第k個節點的位置。時間復雜度為O(n)
代碼實現:(初版)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public Node findLastNode(Node head, int index) { if (node == null) { return null; } Node first = head; Node second = head; //讓second結點往后挪index個位置 for (int i = 0; i < index; i++) { second = second.next; } //讓first和second結點整體向后移動,直到second結點為Nullwhile (second != null) { first = first.next; second = second.next; } //當second結點為空的時候,此時first指向的結點就是我們要找的結點return first;} |
代碼實現:(最終版)(考慮k大于鏈表中結點個數時的情況時,拋出異常)
上面的代碼中,看似已經實現了功能,其實還不夠健壯:
要注意k等于0的情況;
如果k大于鏈表中節點個數時,就會報空指針異常,所以這里需要做一下判斷。
核心代碼如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
public Node findLastNode(Node head, int k) {if (k == 0 || head == null) { return null; } Node first = head; Node second = head;//讓second結點往后挪k-1個位置 for (int i = 0; i < k - 1; i++) { System.out.println("i的值是" + i); second = second.next; if (second == null) { //說明k的值已經大于鏈表的長度了 //throw new NullPointerException("鏈表的長度小于" + k); //我們自己拋出異常,給用戶以提示 return null; }} //讓first和second結點整體向后移動,直到second走到最后一個結點 while (second.next != null) { first = first.next; second = second.next; } //當second結點走到最后一個節點的時候,此時first指向的結點就是我們要找的結點return first;} |
4、查找單鏈表中的中間結點:
同樣,面試官不允許你算出鏈表的長度,該怎么做呢?
思路:
和上面的第2節一樣,也是設置兩個指針first和second,只不過這里是,兩個指針同時向前走,second指針每次走兩步,first指針每次走一步,直到second指針走到最后一個結點時,此時first指針所指的結點就是中間結點。注意鏈表為空,鏈表結點個數為1和2的情況。時間復雜度為O(n)。
代碼實現:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
//方法:查找鏈表的中間結點public Node findMidNode(Node head) {if (head == null) { return null;}Node first = head; Node second = head;//每次移動時,讓second結點移動兩位,first結點移動一位while (second != null && second.next != null) { first = first.next; second = second.next.next;}//直到second結點移動到null時,此時first指針指向的位置就是中間結點的位置 return first;} |
上方代碼中,當n為偶數時,得到的中間結點是第n/2 + 1個結點。比如鏈表有6個節點時,得到的是第4個節點。
5、合并兩個有序的單鏈表,合并之后的鏈表依然有序:
這道題經常被各公司考察。
例如:
鏈表1:
1->2->3->4
鏈表2:
2->3->4->5
合并后:
1->2->2->3->3->4->4->5
解題思路:
挨著比較鏈表1和鏈表2。
這個類似于歸并排序。尤其要注意兩個鏈表都為空、和其中一個為空的情況。只需要O (1) 的空間。時間復雜度為O (max(len1,len2))
代碼實現:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
//兩個參數代表的是兩個鏈表的頭結點public Node mergeLinkList(Node head1, Node head2) {if (head1 == null && head2 == null) { //如果兩個鏈表都為空 return null;} if (head1 == null) { return head2;} if (head2 == null) { return head1;}Node head; //新鏈表的頭結點 Node current; //current結點指向新鏈表 // 一開始,我們讓current結點指向head1和head2中較小的數據,得到head結點 if (head1.data < head2.data) { head = head1; current = head1; head1 = head1.next; } else { head = head2; current = head2; head2 = head2.next;} while (head1 != null && head2 != null) { if (head1.data < head2.data) { current.next = head1; //新鏈表中,current指針的下一個結點對應較小的那個數據 current = current.next; //current指針下移 head1 = head1.next; } else { current.next = head2; current = current.next; head2 = head2.next; } } //合并剩余的元素 if (head1 != null) { //說明鏈表2遍歷完了,是空的 current.next = head1; }if (head2 != null) { //說明鏈表1遍歷完了,是空的 current.next = head2;} return head;} |
代碼測試:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public static void main(String[] args) {LinkList list1 = new LinkList();LinkList list2 = new LinkList();//向LinkList中添加數據for (int i = 0; i < 4; i++) { list1.add(i); }for (int i = 3; i < 8; i++) { list2.add(i);}LinkList list3 = new LinkList();list3.head = list3.mergeLinkList(list1.head, list2.head); //將list1和list2合并,存放到list3中list3.print(list3.head);// 從head節點開始遍歷輸出} |
上方代碼中用到的add方法和print方法和第1小節中是一致的。
運行效果:
注:《劍指offer》中是用遞歸解決的,感覺有點難理解。
6、單鏈表的反轉:【出現頻率最高】
例如鏈表:
1->2->3->4
反轉之后:
4->2->2->1
思路:
從頭到尾遍歷原鏈表,每遍歷一個結點,將其摘下放在新鏈表的最前端。注意鏈表為空和只有一個結點的情況。時間復雜度為O(n)
方法1:(遍歷)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
//方法:鏈表的反轉public Node reverseList(Node head) {//如果鏈表為空或者只有一個節點,無需反轉,直接返回原鏈表的頭結點 if (head == null || head.next == null) { return head;}Node current = head;Node next = null; //定義當前結點的下一個結點 Node reverseHead = null; //反轉后新鏈表的表頭while (current != null) { next = current.next; //暫時保存住當前結點的下一個結點,因為下一次要用 current.next = reverseHead; //將current的下一個結點指向新鏈表的頭結點 reverseHead = current; current = next; // 操作結束后,current節點后移}return reverseHead;} |
上方代碼中,核心代碼是第16、17行。
方法2:(遞歸)
這個方法有點難,先不講了。
7、從尾到頭打印單鏈表:
對于這種顛倒順序的問題,我們應該就會想到棧,后進先出。所以,這一題要么自己使用棧,要么讓系統使用棧,也就是遞歸。注意鏈表為空的情況。時間復雜度為O(n)
注:不要想著先將單鏈表反轉,然后遍歷輸出,這樣會破壞鏈表的結構,不建議。
方法1:(自己新建一個棧)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
//方法:從尾到頭打印單鏈表public void reversePrint(Node head) {if (head == null) { return; } Stack<Node> stack = new Stack<Node>(); //新建一個棧 Node current = head; //將鏈表的所有結點壓棧 while (current != null) {- stack.push(current); //將當前結點壓棧 current = current.next;} //將棧中的結點打印輸出即可while (stack.size() > 0) { System.out.println(stack.pop().data); //出棧操作}} |
方法2:(使用系統的棧:遞歸,代碼優雅簡潔)
|
1
2
3
4
5
6
7
8
9
|
public void reversePrint(Node head) { if (head == null) { return; }reversePrint(head.next);System.out.println(head.data);} |
總結:方法2是基于遞歸實現的,戴安看起來簡潔優雅,但有個問題:當鏈表很長的時候,就會導致方法調用的層級很深,有可能造成棧溢出。而方法1的顯式用棧,是基于循環實現的,代碼的魯棒性要更好一些。
8、判斷單鏈表是否有環:
這里也是用到兩個指針,如果一個鏈表有環,那么用一個指針去遍歷,是永遠走不到頭的。
因此,我們用兩個指針去遍歷:first指針每次走一步,second指針每次走兩步,如果first指針和second指針相遇,說明有環。時間復雜度為O (n)。
方法:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
//方法:判斷單鏈表是否有環public boolean hasCycle(Node head) { if (head == null) { return false; } Node first = head; Node second = head; while (second != null) { first = first.next; //first指針走一步 second = second.next.next; second指針走兩步 if (first == second) { //一旦兩個指針相遇,說明鏈表是有環的 return true; }} return false;} |
完整版代碼:(包含測試部分)
這里,我們還需要加一個重載的add(Node node)方法,在創建單向循環鏈表時要用到。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
LinkList.java: public class LinkList { public Node head; public Node current; //方法:向鏈表中添加數據 public void add(int data) { //判斷鏈表為空的時候 if (head == null) {//如果頭結點為空,說明這個鏈表還沒有創建,那就把新的結點賦給頭結點 head = new Node(data); current = head; } else { //創建新的結點,放在當前節點的后面(把新的結點合鏈表進行關聯) current.next = new Node(data); //把鏈表的當前索引向后移動一位 current = current.next; } } //方法重載:向鏈表中添加結點 public void add(Node node) { if (node == null) { return; } if (head == null) { head = node; current = head; } else { current.next = node; current = current.next; } } //方法:遍歷鏈表(打印輸出鏈表。方法的參數表示從節點node開始進行遍歷 public void print(Node node) { if (node == null) { return; } current = node; while (current != null) { System.out.println(current.data); current = current.next; } } //方法:檢測單鏈表是否有環 public boolean hasCycle(Node head) { if (head == null) { return false; } Node first = head; Node second = head; while (second != null) { first = first.next; //first指針走一步 second = second.next.next; //second指針走兩步 if (first == second) { //一旦兩個指針相遇,說明鏈表是有環的 return true; } } return false; } class Node { //注:此處的兩個成員變量權限不能為private,因為private的權限是僅對本類訪問。 int data; //數據域 Node next;//指針域 public Node(int data) { this.data = data; } } public static void main(String[] args) { LinkList list = new LinkList(); //向LinkList中添加數據 for (int i = 0; i < 4; i++) { list.add(i); } list.add(list.head); //將頭結點添加到鏈表當中,于是,單鏈表就有環了。備注:此時得到的這個環的結構,是下面的第8小節中圖1的那種結構。 System.out.println(list.hasCycle(list.head)); } } |
檢測單鏈表是否有環的代碼是第50行。
88行:我們將頭結點繼續往鏈表中添加,此時單鏈表就環了。最終運行效果為true。
如果刪掉了88行代碼,此時單鏈表沒有環,運行效果為false。
9、取出有環鏈表中,環的長度:
我們平時碰到的有環鏈表是下面的這種:(圖1)
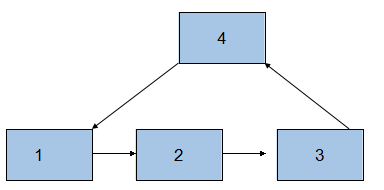
上圖中環的長度是4。
但有可能也是下面的這種:(圖2)

此時,上圖中環的長度就是3了。
那怎么求出環的長度呢?
思路:
這里面,我們需要先利用上面的第7小節中的hasCycle方法(判斷鏈表是否有環的那個方法),這個方法的返回值是boolean型,但是現在要把這個方法稍做修改,讓其返回值為相遇的那個結點。然后,我們拿到這個相遇的結點就好辦了,這個結點肯定是在環里嘛,我們可以讓這個結點對應的指針一直往下走,直到它回到原點,就可以算出環的長度了。
方法:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
//方法:判斷單鏈表是否有環。返回的結點是相遇的那個結點public Node hasCycle(Node head) { if (head == null) { return null; } Node first = head; Node second = head;while (second != null) { first = first.next; second = second.next.next; if (first == second) { //一旦兩個指針相遇,說明鏈表是有環的 return first; //將相遇的那個結點進行返回 } } return null;}//方法:有環鏈表中,獲取環的長度。參數node代表的是相遇的那個結點public int getCycleLength(Node node) { if (head == null) { return 0; } Node current = node; int length = 0; while (current != null) { current = current.next; length++; if (current == node) { //當current結點走到原點的時候 return length; } } return length;} |
完整版代碼:(包含測試部分)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
|
public class LinkList { public Node head; public Node current; public int size; //方法:向鏈表中添加數據 public void add(int data) { //判斷鏈表為空的時候 if (head == null) {//如果頭結點為空,說明這個鏈表還沒有創建,那就把新的結點賦給頭結點 head = new Node(data); current = head; } else { //創建新的結點,放在當前節點的后面(把新的結點合鏈表進行關聯) current.next = new Node(data); //把鏈表的當前索引向后移動一位 current = current.next; //此步操作完成之后,current結點指向新添加的那個結點 } } //方法重載:向鏈表中添加結點 public void add(Node node) { if (node == null) { return; } if (head == null) { head = node; current = head; } else { current.next = node; current = current.next; } } //方法:遍歷鏈表(打印輸出鏈表。方法的參數表示從節點node開始進行遍歷 public void print(Node node) { if (node == null) { return; } current = node; while (current != null) { System.out.println(current.data); current = current.next; } } //方法:判斷單鏈表是否有環。返回的結點是相遇的那個結點 public Node hasCycle(Node head) { if (head == null) { return null; } Node first = head; Node second = head; while (second != null) { first = first.next; second = second.next.next; if (first == second) { //一旦兩個指針相遇,說明鏈表是有環的 return first; //將相遇的那個結點進行返回 } } return null; } //方法:有環鏈表中,獲取環的長度。參數node代表的是相遇的那個結點 public int getCycleLength(Node node) { if (head == null) { return 0; } Node current = node; int length = 0; while (current != null) { current = current.next; length++; if (current == node) { //當current結點走到原點的時候 return length; } } return length; } class Node { //注:此處的兩個成員變量權限不能為private,因為private的權限是僅對本類訪問。 int data; //數據域 Node next;//指針域 public Node(int data) { this.data = data; } } public static void main(String[] args) { LinkList list1 = new LinkList(); Node second = null; //把第二個結點記下來 //向LinkList中添加數據 for (int i = 0; i < 4; i++) { list1.add(i); if (i == 1) { second = list1.current; //把第二個結點記下來 } } list1.add(second); //將尾結點指向鏈表的第二個結點,于是單鏈表就有環了,備注:此時得到的環的結構,是本節中圖2的那種結構 Node current = list1.hasCycle(list1.head); //獲取相遇的那個結點 System.out.println("環的長度為" + list1.getCycleLength(current)); } } |
運行效果:
如果將上面的104至122行的測試代碼改成下面這樣的:(即:將圖2中的結構改成圖1中的結構)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public static void main(String[] args) { LinkList list1 = new LinkList(); //向LinkList中添加數據 for (int i = 0; i < 4; i++) { list1.add(i); } list1.add(list1.head); //將頭結點添加到鏈表當中(將尾結點指向頭結點),于是,單鏈表就有環了。備注:此時得到的這個環的結構,是本節中圖1的那種結構。 Node current = list1.hasCycle(list1.head); System.out.println("環的長度為" + list1.getCycleLength(current)); } |
運行結果:
如果把上面的代碼中的第8行刪掉,那么這個鏈表就沒有環了,于是運行的結果為0。
10、單鏈表中,取出環的起始點:
我們平時碰到的有環鏈表是下面的這種:(圖1)
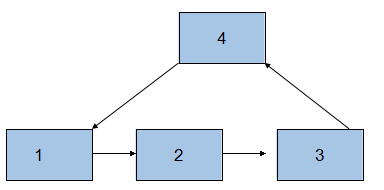
上圖中環的起始點1。
但有可能也是下面的這種:(圖2)
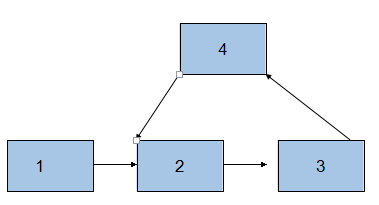
此時,上圖中環的起始點是2。
方法1:
這里我們需要利用到上面第8小節的取出環的長度的方法getCycleLength,用這個方法來獲取環的長度length。拿到環的長度length之后,需要用到兩個指針變量first和second,先讓second指針走length步;然后讓first指針和second指針同時各走一步,當兩個指針相遇時,相遇時的結點就是環的起始點。
注:為了找到環的起始點,我們需要先獲取環的長度,而為了獲取環的長度,我們需要先判斷是否有環。所以這里面其實是用到了三個方法。
代碼實現:
方法1的核心代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
//方法:獲取環的起始點。參數length表示環的長度public Node getCycleStart(Node head, int cycleLength) { if (head == null) { return null; } Node first = head; Node second = head; //先讓second指針走length步 for (int i = 0; i < cycleLength; i++) { second = second.next; } //然后讓first指針和second指針同時各走一步 while (first != null && second != null) { first = first.next; second = second.next; if (first == second) { //如果兩個指針相遇了,說明這個結點就是環的起始點 return first; } } return null; } |
完整版代碼:(含測試部分)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
|
public class LinkList { public Node head; public Node current; public int size; //方法:向鏈表中添加數據 public void add(int data) { //判斷鏈表為空的時候 if (head == null) {//如果頭結點為空,說明這個鏈表還沒有創建,那就把新的結點賦給頭結點 head = new Node(data); current = head; } else { //創建新的結點,放在當前節點的后面(把新的結點合鏈表進行關聯) current.next = new Node(data); //把鏈表的當前索引向后移動一位 current = current.next; //此步操作完成之后,current結點指向新添加的那個結點 } } //方法重載:向鏈表中添加結點 public void add(Node node) { if (node == null) { return; } if (head == null) { head = node; current = head; } else { current.next = node; current = current.next; } } //方法:遍歷鏈表(打印輸出鏈表。方法的參數表示從節點node開始進行遍歷 public void print(Node node) { if (node == null) { return; } current = node; while (current != null) { System.out.println(current.data); current = current.next; } } //方法:判斷單鏈表是否有環。返回的結點是相遇的那個結點 public Node hasCycle(Node head) { if (head == null) { return null; } Node first = head; Node second = head; while (second != null) { first = first.next; second = second.next.next; if (first == second) { //一旦兩個指針相遇,說明鏈表是有環的 return first; //將相遇的那個結點進行返回 } } return null; } //方法:有環鏈表中,獲取環的長度。參數node代表的是相遇的那個結點 public int getCycleLength(Node node) { if (head == null) { return 0; } Node current = node; int length = 0; while (current != null) { current = current.next; length++; if (current == node) { //當current結點走到原點的時候 return length; } } return length; } //方法:獲取環的起始點。參數length表示環的長度 public Node getCycleStart(Node head, int cycleLength) { if (head == null) { return null; } Node first = head; Node second = head; //先讓second指針走length步 for (int i = 0; i < cycleLength; i++) { second = second.next; } //然后讓first指針和second指針同時各走一步 while (first != null && second != null) { first = first.next; second = second.next; if (first == second) { //如果兩個指針相遇了,說明這個結點就是環的起始點 return first; } } return null; } class Node { //注:此處的兩個成員變量權限不能為private,因為private的權限是僅對本類訪問。 int data; //數據域 Node next;//指針域 public Node(int data) { this.data = data; } } public static void main(String[] args) { LinkList list1 = new LinkList(); Node second = null; //把第二個結點記下來 //向LinkList中添加數據 for (int i = 0; i < 4; i++) { list1.add(i); if (i == 1) { second = list1.current; //把第二個結點記下來 } } list1.add(second); //將尾結點指向鏈表的第二個結點,于是單鏈表就有環了,備注:此時得到的環的結構,是本節中圖2的那種結構 Node current = list1.hasCycle(list1.head); //獲取相遇的那個結點 int length = list1.getCycleLength(current); //獲取環的長度 System.out.println("環的起始點是" + list1.getCycleStart(list1.head, length).data); }} |
11、判斷兩個單鏈表相交的第一個交點:
《編程之美》P193,5.3,面試題37就有這道題。
面試時,很多人碰到這道題的第一反應是:在第一個鏈表上順序遍歷每個結點,每遍歷到一個結點的時候,在第二個鏈表上順序遍歷每個結點。如果在第二個鏈表上有一個結點和第一個鏈表上的結點一樣,說明兩個鏈表在這個結點上重合。顯然該方法的時間復雜度為O(len1 * len2)。
方法1:采用棧的思路
我們可以看出兩個有公共結點而部分重合的鏈表,拓撲形狀看起來像一個Y,而不可能是X型。 如下圖所示:
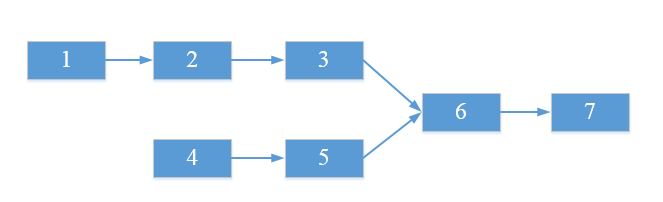
如上圖所示,如果單鏈表有公共結點,那么最后一個結點(結點7)一定是一樣的,而且是從中間的某一個結點(結點6)開始,后續的結點都是一樣的。
現在的問題是,在單鏈表中,我們只能從頭結點開始順序遍歷,最后才能到達尾結點。最后到達的尾節點卻要先被比較,這聽起來是不是像“先進后出”?于是我們就能想到利用棧的特點來解決這個問題:分別把兩個鏈表的結點放入兩個棧中,這樣兩個鏈表的尾結點就位于兩個棧的棧頂,接下來比較下一個棧頂,直到找到最后一個相同的結點。
這種思路中,我們需要利用兩個輔助棧,空間復雜度是O(len1+len2),時間復雜度是O(len1+len2)。和一開始的蠻力法相比,時間效率得到了提高,相當于是利用空間消耗換取時間效率。
那么,有沒有更好的方法呢?接下來要講。
方法2:判斷兩個鏈表相交的第一個結點:用到快慢指針,推薦(更優解)
我們在上面的方法2中,之所以用到棧,是因為我們想同時遍歷到達兩個鏈表的尾結點。其實為解決這個問題我們還有一個更簡單的辦法:首先遍歷兩個鏈表得到它們的長度。在第二次遍歷的時候,在較長的鏈表上走 |len1-len2| 步,接著再同時在兩個鏈表上遍歷,找到的第一個相同的結點就是它們的第一個交點。
這種思路的時間復雜度也是O(len1+len2),但是我們不再需要輔助棧,因此提高了空間效率。當面試官肯定了我們的最后一種思路的時候,就可以動手寫代碼了。
核心代碼:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
//方法:求兩個單鏈表相交的第一個交點public Node getFirstCommonNode(Node head1, Node head2) { if (head1 == null || head == null) { return null; } int length1 = getLength(head1); int length2 = getLength(head2); int lengthDif = 0; //兩個鏈表長度的差值 Node longHead; Node shortHead; //找出較長的那個鏈表 if (length1 > length2) { longHead = head1; shortHead = head2; lengthDif = length1 - length2; } else { longHead = head2; shortHead = head1; lengthDif = length2 - length1; } //將較長的那個鏈表的指針向前走length個距離 for (int i = 0; i < lengthDif; i++) { longHead = longHead.next; } //將兩個鏈表的指針同時向前移動 while (longHead != null && shortHead != null) { if (longHead == shortHead) { //第一個相同的結點就是相交的第一個結點 return longHead; } longHead = longHead.next; shortHead = shortHead.next; } return null;}//方法:獲取單鏈表的長度public int getLength(Node head) { if (head == null) { return 0; } int length = 0;Node current = head; while (current != null) { length++; current = current.next; } return length; |
以上就是有關java鏈表的經典面試題目,希望可以幫助大家順利通過面試。














