引子

1. 向量刻畫的是線性空間中的對象。
2. 矩陣刻畫的是向量在線性空間中的運動（變換，躍遷），相似矩陣本質(zhì)上就是同一個線性變換的不同的描述。
3. 在一個線性空間中，選定了一組基，對于任何一個線性變化都可以用一個確定的矩陣來描述
4. 矩陣不僅可以作為線性變換的描述，而且可以作為一組基的描述，作為變換的矩陣，不但可以把線性空間中的一個點給變換到另一個點去，而且也能夠把線性空間中的一個坐標(biāo)系（基）表換到另一個坐標(biāo)系（基）去。
5. 當(dāng)我們談到向量時，一定要指定它所在的坐標(biāo)系才有意義，比如向量b=(1,2,3)實際上指的是在單位坐標(biāo)系I下有一個向量的度量為b。
6. 就可以理解Ma=b就可以看成Ma=Ib，就是說在坐標(biāo)系M中度量出來的向量a和在坐標(biāo)系I里面度量出來的b實際上就是同一個向量。
7. 對于矩陣而言，他表示出來的那個坐標(biāo)系也是由一組基（向量）組成的，同樣存在這組基實在哪個坐標(biāo)系下度量的問題。對于矩陣M，將其理解成IM，即M中的那組向量是在I坐標(biāo)系中得出的。
8. MxN本質(zhì)是聲明了一個在M坐標(biāo)系中量出的另一個坐標(biāo)系N，其中M本身是在I坐標(biāo)系中度量出來的。
9. 對坐標(biāo)系施加變換的方法，就是讓表示那個坐標(biāo)系的矩陣與表示那個變化的矩陣相乘。

因此我們來理解這樣一個式子，ACb,AC為矩陣，b為一個向量

• b是一個向量，他是在I坐標(biāo)系下度量的，a = Cb也就是在I坐標(biāo)系下將向量b變換到向量b，d=ACb=Aa的含義就是繼續(xù)在I坐標(biāo)系下將向量a變換到向量d。即在同一個坐標(biāo)系I下面進(jìn)行了兩次變換操作。
• 另一種理解方式是ACb=IACb，那么IAC三個矩陣相乘就表示了坐標(biāo)系的變換，在I坐標(biāo)系中度量處新的坐標(biāo)系IA，再在IA坐標(biāo)系下度量出IAC，然后這里最終的坐標(biāo)系中的向量b和在1中在I坐標(biāo)系中經(jīng)過兩次變換得到的向量是同一個向量。

上面的兩種理解方式也揭示了對向量的變換和對坐標(biāo)系的變換是等價的，這一點也可以通過后面旋轉(zhuǎn)變換的圖示中看出來。

各種變換

平移矩陣

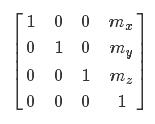
縮放矩陣

平移矩陣和縮放矩陣很容易理解，并且從矩陣形式我們也可以看到為什么用四維的向量表示一個頂點了，除了w分量用來做透視除法以外，另一個作用不也正好是為了把平移整合進(jìn)來嗎，都做乘法而不做加法。在數(shù)學(xué)上也就是將三維空間的坐標(biāo)表示成其齊次形式.

旋轉(zhuǎn)變換

旋轉(zhuǎn)變換相對來說較為復(fù)雜，對繞x、y或z軸旋轉(zhuǎn)的情況比較好理解。

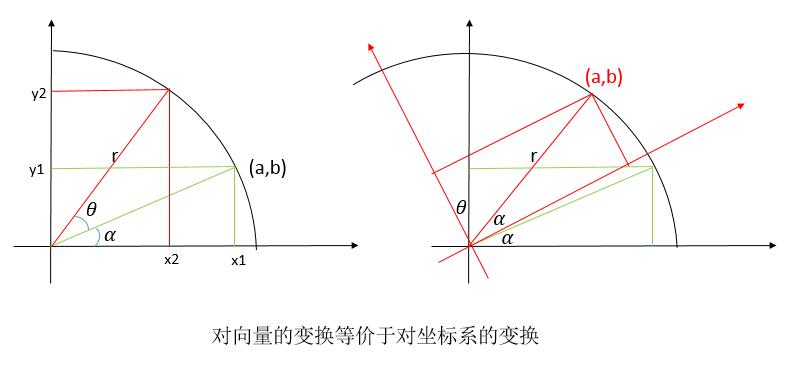
以繞z軸旋轉(zhuǎn)為例

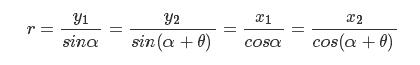
于是

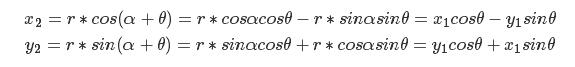
寫成矩陣形式為

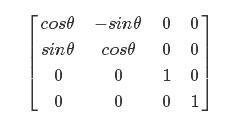
繞任意軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣為

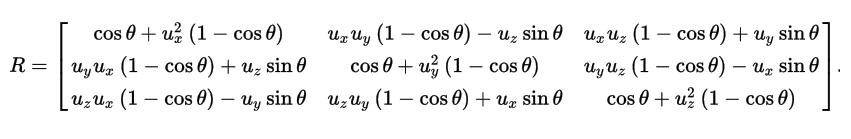
同理，前面學(xué)到的正交投影矩陣，透視矩陣以及攝像機矩陣，本質(zhì)上和上面的變換都是一樣的。

前面可以看到一般傳入渲染管線的是一個由攝像機矩陣，投影矩陣，變換矩陣相乘得到的總的變換矩陣，

在頂點著色器中一般是這樣的形式

上面的代碼中的變量uMVPMatrix表示了模型（M）、視圖（V）、投影（P）三中變換綜合，

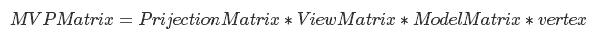
注意到矩陣乘法的順序，對每個點所做的變換是有順序的，對每個點先進(jìn)行模型變換（平移縮放旋轉(zhuǎn)）、再進(jìn)行視圖變換（攝像機視角）再進(jìn)行投影變換，這三個變換順序是不可變得，因為改變順序最終看到的效果都是不一樣的。

對每個點所做的綜合變換本質(zhì)上就是對這個點進(jìn)行矩陣相乘，然而就我們傳入的是最終的綜合變換矩陣而言，剛才的理解不是特別準(zhǔn)確，換個思路理解成綜合變換矩陣就是對坐標(biāo)系的變換會更好，因為畢竟我們是一次性將這個相乘后的綜合矩陣傳進(jìn)去的。

以上就是本文的全部內(nèi)容，希望對大家的學(xué)習(xí)有所幫助，也希望大家多多支持服務(wù)器之家。

原文鏈接：https://blog.csdn.net/cauchyweierstrass/article/details/52909609