歸并排序
歸并,指合并,合在一起。歸并排序(Merge Sort)是建立在歸并操作上的一種排序算法。其主要思想是分而治之。什么是分而治之?分而治之就是將一個復雜的計算,按照設定的閾值進行分解成多個計算,然后將各個計算結果進行匯總。即“分”就是把一個大的通過遞歸拆成若干個小的,“治”就是將分后的結果在合在一起。
若將兩個有序集合并成一個有序表,稱為2-路歸并,與之對應的還有多路歸并。
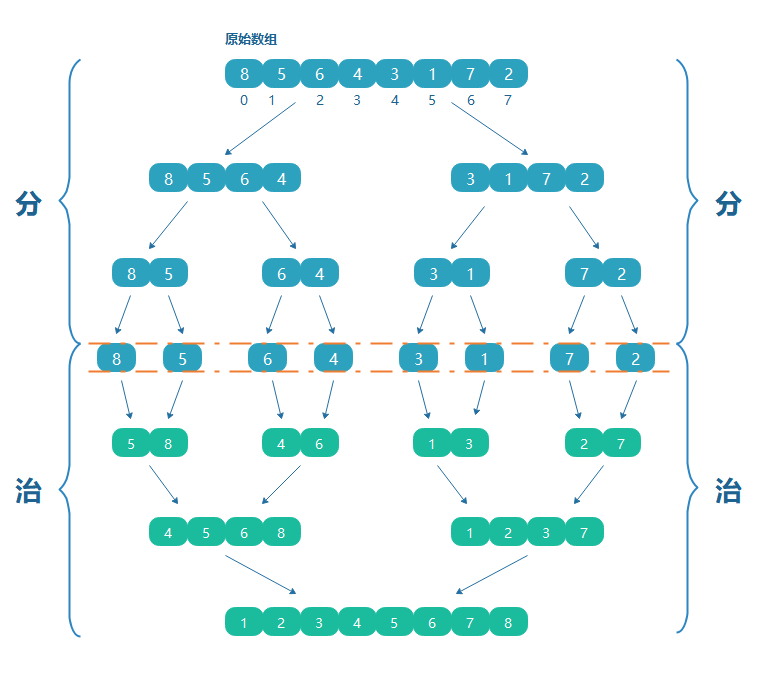
怎么分
- 對于排序最好的情況來講,就是只有兩個元素,這時候比較大小就很簡單,但是還是需要比較
- 如果拆分為左右各一個,無需比較即是有序的。
怎么治
借助一個輔助空數組,把左右兩邊的數組按照大小比較,按順序放入輔助數組中即可。
以下面兩個有序數組為例:
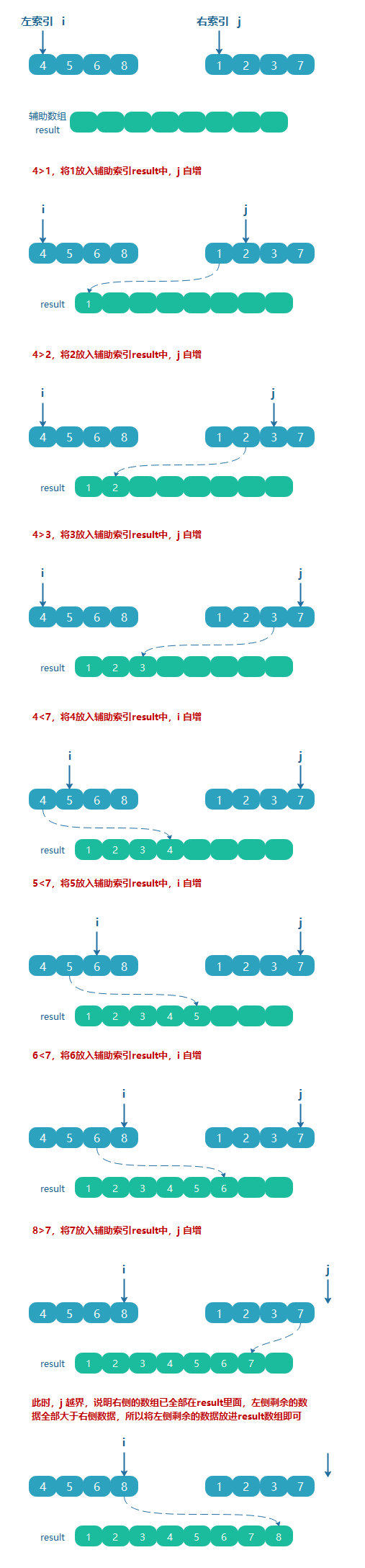
代碼實現
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
public class MergeSort { public static final int[] ARRAY = {8, 5, 6, 4, 3, 1, 7, 2}; public static int[] sort(int[] array) { if (array.length < 2) return array; int mid = array.length / 2; //分成2組 int[] left = Arrays.copyOfRange(array, 0, mid); int[] right = Arrays.copyOfRange(array, mid, array.length); //遞歸拆分 return merge(sort(left), sort(right)); } //治---合并 public static int[] merge(int[] left, int[] right) { int[] result = new int[left.length + right.length]; //i代表左邊數組的索引,j代表右邊 for (int index = 0, i = 0, j = 0; index < result.length; index++) { if (i >= left.length) {//說明左側的數據已經全部取完,取右邊的數據 result[index] = right[j++]; } else if (j >= right.length) {//說明右側的數據已經全部取完,取左邊的數據 result[index] = left[i++]; } else if (left[i] > right[j]) {//左邊大于右邊,取右邊的 int a = right[j++]; result[index] = a; } else {//右邊大于左邊,取左邊的 result[index] = left[i++]; } } return result; } public static void print(int[] array) { for (int i : array) { System.out.print(i + " "); } System.out.println(""); } public static void main(String[] args) { print(ARRAY); System.out.println("============================================"); print(sort(ARRAY)); }} |
時間復雜度
歸并排序方法就是把一組n個數的序列,折半分為兩個序列,然后再將這兩個序列再分,一直分下去,直到分為n個長度為1的序列。然后兩兩按大小歸并。如此反復,直到最后形成包含n個數的一個數組。
歸并排序總時間 = 分解時間 + 子序列排好序時間 + 合并時間
無論每個序列有多少數都是折中分解,所以分解時間是個常數,可以忽略不計,則:
歸并排序總時間 = 子序列排好序時間 + 合并時間
假設處理的數據規(guī)模大小為 n,運行時間設為:T(n),則T(n) = n,當 n = 1時,T(1) = 1
由于在合并時,兩個子序列已經排好序,所以在合并的時候只需要 if 判斷即可,所以n個數比較,合并的時間復雜度為 n。
- 將 n 個數的序列,分為兩個 n/2 的序列,則:T(n) = 2T(n/2) + n
- 將 n/2 個數的序列,分為四個 n/4 的序列,則:T(n) = 4T(n/4) + 2n
- 將 n/4 個數的序列,分為八個 n/8 的序列,則:T(n) = 8T(n/8) + 3n
- …
- 將 n/2k 個數的序列,分為2k個 n/2k 的序列,則:T(n) = 2kT(n/2k) + kn
當 T(n/2k) = T(1)時, 即n/2k = 1(此時也是把n分解到只有1個數據的時候),轉換為以2為底n的對數:k = log2n,把k帶入到T(n)中,得:T(n) = n + nlog2n。
使用大O表示法,去掉常數項 n,省略底數 2,則歸并排序的時間復雜度為:O(nlogn)
算法穩(wěn)定性
從原理分析和代碼可以看出,為在合并的時候,如果相等,選擇前面的元素到輔助數組,所以歸并排序是穩(wěn)定的。
總結
本篇文章就到這里了,希望能給你帶來幫助,也希望您能夠多多關注服務器之家的更多內容!
原文鏈接:https://blog.csdn.net/weixin_43477531/article/details/119821587