希爾排序
一種基于插入排序的快速的排序算法。簡單插入排序對于大規模亂序數組很慢,因為元素只能一點一點地從數組的一端移動到另一端。例如,如果主鍵最小的元素正好在數組的盡頭,要將它挪到正確的位置就需要n-1次移動。
希爾排序為了加快速度簡單地改進了插入排序,也稱為縮小增量排序。
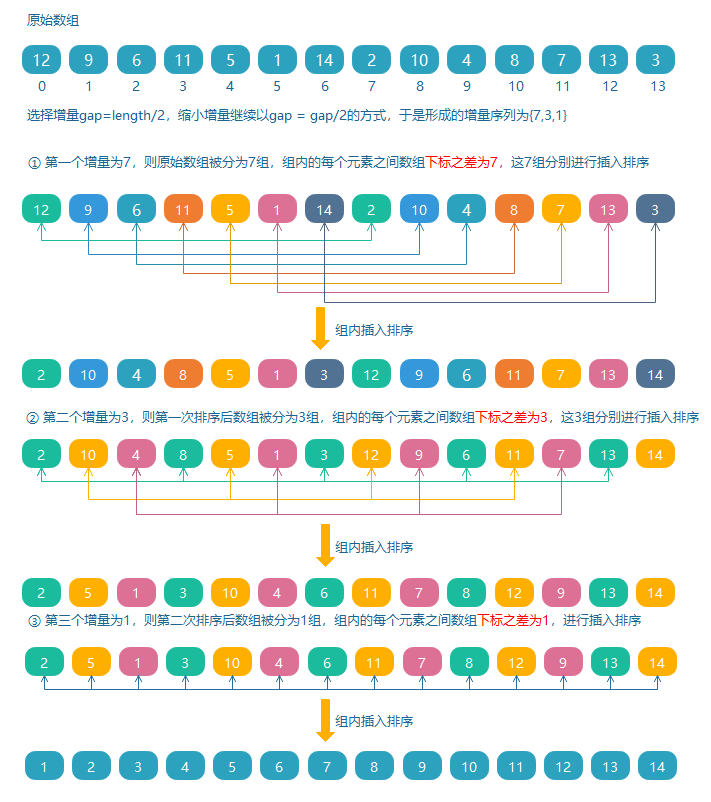
希爾排序是把待排序數組按一定的數量分組,對每組使用直接插入排序算法排序;然后縮小數量繼續分組排序,隨著數量逐漸減少,每組包含的元素越來越多,當數量減至 1 時,整個數組恰被分成一組,排序便完成了。這個不斷縮小的數量,就構成了一個增量序列,這里的數量稱為增量。
代碼實現
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
public class ShellSort { public static final int[] ARRAY = {12, 9, 6, 11, 5, 1, 14, 2, 10, 4, 8, 7, 13, 3}; public static int[] sort(int[] array) { int len = array.length; if (len < 2) { return array; } //當前待排序數據,該數據之前的已被排序 int current; //增量 int gap = len / 2; while (gap > 0) { for (int i = gap; i < len; i++) { current = array[i]; //前面有序序列的索引 int index = i - gap; while (index >= 0 && current < array[index]) { array[index + gap] = array[index]; //有序序列的下一個 index -= gap; } //插入 array[index + gap] = current; } //int相除取整 gap = gap / 2; } return array; } public static void print(int[] array) { for (int i : array) { System.out.print(i + " "); } System.out.println(""); } public static void main(String[] args) { print(ARRAY); System.out.println("============================================"); print(sort(ARRAY)); }} |
時間復雜度
希爾排序的復雜度和增量序列有關。
在先前較大的增量下每個子序列的規模都不大,用直接插入排序效率都較高,盡管在隨后的增量遞減分組中子序列越來越大,由于整個序列的有序性也越來越明顯,則排序效率依然較高。
從理論上說,只要一個數組是遞減的,并且最后一個值是1,都可以作為增量序列使用。有沒有一個步長序列,使得排序過程中所需的比較和移動次數相對較少,并且無論待排序列記錄數有多少,算法的時間復雜度都能漸近最佳呢?但是目前從數學上來說,無法證明某個序列是最好的。
常用的增量序列:
- 希爾增量序列 :{n/2, (n / 2)/2, …, 1},其中N為原始數組的長度,這是最常用的序列,但卻不是最好的
- Hibbard序列:{2k-1, …, 3,1}
- Sedgewick序列:{… , 109 , 41 , 19 , 5,1} 表達式為9 * 4i- 9 * 2i + 1,i = 0,1,2,3,4…
算法穩定性
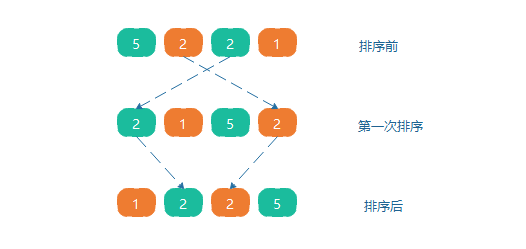
由于多次插入排序,我們知道一次插入排序是穩定的,不會改變相同元素的相對順序,但在不同的插入排序過程中,相同的元素可能在各自的插入排序中移動,如數組5,2,2,1,第一次排序第一個元素5會和第三個元素2交換,第二個元素2會和第四個元素1交換,原序列中兩個2的相對前后順序就被破壞了,所以希爾排序是一個不穩定的排序算法。
總結
本篇文章就到這里了,希望能給你帶來幫助,也希望您能夠多多關注服務器之家的更多內容!
原文鏈接:https://blog.csdn.net/weixin_43477531/article/details/119821587