本文實例為大家分享了java計算圖兩點之間的所有路徑的具體代碼,供大家參考,具體內容如下
1.給定圖如下:
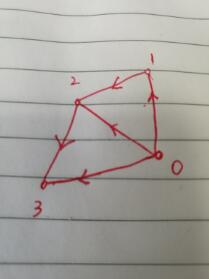
2.求0到3之間可達的所有路徑
這里問題就是關于搜索遍歷的問題,但其中需要注意到不能產生回路或環.
算法描述如下:
top_node:當前棧頂元素
adjvex_node;當前top_node已經訪問的鄰接點
next_node:即將訪問的元素(top_node的第adjvex_node個鄰接點所對應的元素)
找出所有路徑采用的是遍歷的方法,以“深度優先”算法為基礎。從源點出發,先到源點的第一個鄰接點n00,再到n00的第一個鄰接點n10,再到n10的第一個鄰接點n20...當遍歷到目標點時表明找到一條路徑。
上述代碼的核心數據結構為一個棧,主要步驟:
①源點先入棧,并進行標記
②獲取棧頂元素top_node,如果棧頂為終點時,即找到一條路徑,棧頂元素top_node出棧,此時adjvex_node=top_node,新的棧頂元素為top_node,否則執行③
③從top_node的所有鄰接點中,從adjvex_node為起點,選取下一個鄰接點next_node;如果該元素非空,則入棧,使得adjvex_node=-1,(adjvex_node=-1代表top_node的鄰接點一個還沒有訪問)做入棧標記。否則代表沒有后續節點了,此時必須出棧棧頂元素,并置adjvex_node為該棧頂元素,并做出棧標記。
④為避免回路,已入棧元素要記錄,選取新入棧頂點時應跳過已入棧的頂點,當棧為空時,遍歷完成
3.java代碼實現
1)圖結構
點表
|
1
2
3
4
5
6
|
public class vertex {//存放點信息public int data;//與該點鄰接的第一個邊節點public edge firstedge;} |
邊表(代表與點相連的點的集合)
|
1
2
3
4
5
6
7
8
9
10
|
//邊節點public class edge {//對應的點下表public int vertexid;//邊的權重public int weight;//下一個邊節點public edge next;//getter and setter自行補充} |
2).算法實現
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
|
import java.util.hashmap;import java.util.map;import java.util.stack;public class graph {public vertex[] vertexlist; //存放點的集合public graph(int vertexnum){ this.vertexnum=vertexnum; vertexlist=new vertex[vertexnum];}//點個數public int vertexnum;//邊個數public int edgelength;public void initvertext(int datas[]){ for(int i=0;i<vertexnum;i++){ vertex vertext=new vertex(); vertext.data=datas[i]; vertext.firstedge=null; vertexlist[i]=vertext; //system.out.println("i"+vertexlist[i]); } isvisited=new boolean[vertexnum]; for(int i=0;i<isvisited.length;i++){ isvisited[i]=false; }}//針對x節點添加邊節點ypublic void addedge(int x,int y,int weight){ edge edge=new edge(); edge.setvertexid(y); edge.setweight(weight); //第一個邊節點 system.out.println(vertexlist.length); if(null==vertexlist[x].firstedge){ vertexlist[x].firstedge=edge; edge.setnext(null); } //不是第一個邊節點,則采用頭插法 else{ edge.next=vertexlist[x].firstedge; vertexlist[x].firstedge=edge; }}//得到x的鄰接點為y的后一個鄰接點位置,為-1說明沒有找到public int getnextnode(int x,int y){ int next_node=-1; edge edge=vertexlist[x].firstedge; if(null!=edge&&y==-1){ int n=edge.vertexid; //元素還不在stack中 if(!states.get(n)) return n; return -1; } while(null!=edge){ //節點未訪問 if(edge.vertexid==y){ if(null!=edge.next){ next_node=edge.next.vertexid; if(!states.get(next_node)) return next_node; } else return -1; } edge=edge.next; } return -1;}//代表某節點是否在stack中,避免產生回路public map<integer,boolean> states=new hashmap(); //存放放入stack中的節點public stack<integer> stack=new stack(); //輸出2個節點之間的輸出路徑public void visit(int x,int y){ //初始化所有節點在stack中的情況 for(int i=0;i<vertexnum;i++){ states.put(i,false); } //stack top元素 int top_node; //存放當前top元素已經訪問過的鄰接點,若不存在則置-1,此時代表訪問該top元素的第一個鄰接點 int adjvex_node=-1; int next_node; stack.add(x); states.put(x,true); while(!stack.isempty()){ top_node=stack.peek(); //找到需要訪問的節點 if(top_node==y){ //打印該路徑 printpath(); adjvex_node=stack.pop(); states.put(adjvex_node,false); } else{ //訪問top_node的第advex_node個鄰接點 next_node=getnextnode(top_node,adjvex_node); if(next_node!=-1){ stack.push(next_node); //置當前節點訪問狀態為已在stack中 states.put(next_node,true); //臨接點重置 adjvex_node=-1; } //不存在臨接點,將stack top元素退出 else{ //當前已經訪問過了top_node的第adjvex_node鄰接點 adjvex_node=stack.pop(); //不在stack中 states.put(adjvex_node,false); } } }} //打印stack中信息,即路徑信息 public void printpath(){ stringbuilder sb=new stringbuilder(); for(integer i :stack){ sb.append(i+"->"); } sb.delete(sb.length()-2,sb.length()); system.out.println(sb.tostring());} public static void main(string[]args){ graph g=new graph(5); g.initvertext(new int[]{1,2,3,4,4}); //system.out.println(g.vertexlist[0]); g.addedge(0,1,1); g.addedge(0,2,3); g.addedge(0,3,4); g.addedge(1,2,1); g.addedge(2,0,1); g.addedge(2,3,1); g.addedge(1,3,2); g.visit(0,3);}} |
執行結果如下:
0->3
0->2->3
0->1->2->3
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:https://blog.csdn.net/xqhadoop/article/details/66476728