為什么需要樹這種結構
1.數組存儲方式分析:
- 優點:通過下標方式訪問元素,速度快。對于有序數組,還可以使用二分查找提高檢索速度。
- 缺點:如果檢索某個具體的值,或者插入值(按一定的順序)會整體移動,效率較低。
2.鏈式存儲方式分析:
- 優點:在一定程度上對數組存儲方式優化(比如:插入一個數值節點,只需要將插入節點,鏈接到鏈表中即可,刪除效率很高)。
- 缺點:在進行檢索時,效率仍然很低,需要從頭結點開始遍歷。
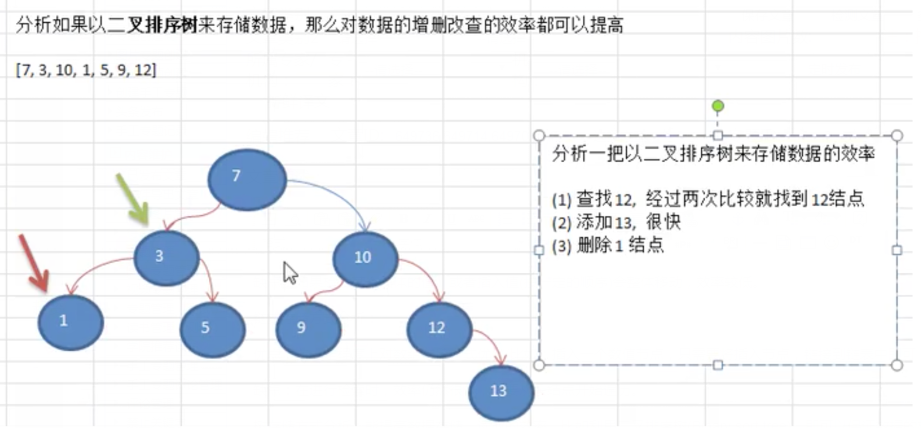
3.樹存儲方式分析:能提高數據存儲,讀取的效率,比如利用二叉排序樹(Binary sort tree),即可以保證數據的檢索速度,同時也可以保證數據的插入、刪除、修改的速度。假設一組[7,3,10,1,5,9,12]以樹的方式存儲,分析如下圖:
二叉樹的前序遍歷、中序遍歷、后序遍歷
- 前序遍歷:輸出父節點、輸出左邊節點、輸出右邊節點;
- 中序遍歷:輸出左邊節點、輸出父節點、輸出右邊節點;
- 后序遍歷:輸出左邊節點、輸出右邊節點、輸出父節點;
需求案例
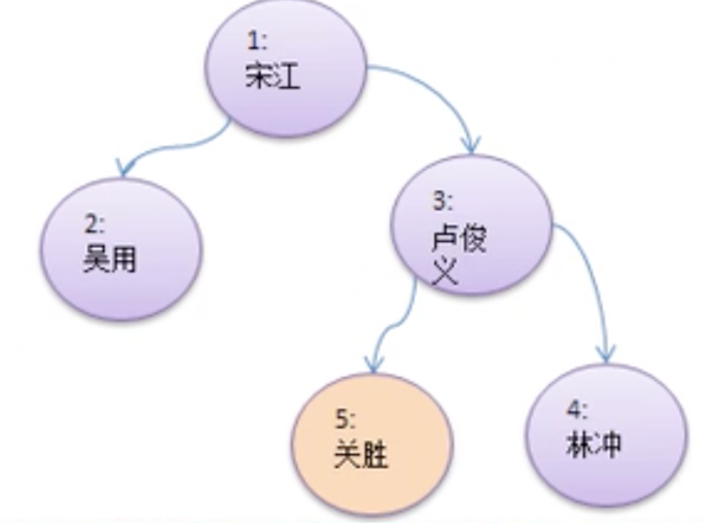
完成一個如下二叉樹節點存儲、前序遍歷搜索、中序遍歷搜索、后序遍歷搜索和刪除節點功能。
對于刪除節點要求如下:
- 如果刪除的節點是葉子節點,則刪除該節點。
- 如果刪除的節點是非葉子節點,則刪除該樹。
- 測試,刪除5號葉子節點和3號子樹。
代碼案例
package com.xie.tree;
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吳用");
HeroNode node3 = new HeroNode(3, "盧俊義");
HeroNode node4 = new HeroNode(4, "林沖");
HeroNode node5 = new HeroNode(5, "關勝");
//先手動創建該二叉樹,后面用遞歸方式
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//前序遍歷
System.out.println("前序遍歷");
binaryTree.preOrder();
//中序遍歷
System.out.println("中序遍歷");
binaryTree.infixOrder();
//后續遍歷
System.out.println("后續遍歷");
binaryTree.postOrder();
//前序遍歷查找
System.out.println("前序遍歷查找~~");
HeroNode resultNode = binaryTree.preOrderSearch(5);
if (resultNode != null) {
System.out.printf("找到了,信息為no=%d,name=%s\n", resultNode.getNo(), resultNode.getName());
System.out.println("遍歷次數:" + HeroNode.preCount);
} else {
System.out.println("沒有找到");
}
//中序遍歷查找
System.out.println("中序遍歷查找~~");
HeroNode resultNode1 = binaryTree.infixOrderSearch(5);
if (resultNode1 != null) {
System.out.printf("找到了,信息為no=%d,name=%s\n", resultNode1.getNo(), resultNode1.getName());
System.out.println("遍歷次數:" + HeroNode.infoxCount);
} else {
System.out.println("沒有找到");
}
//后序遍歷查找
System.out.println("后序遍歷查找~~");
HeroNode resultNode2 = binaryTree.postOrderSearch(5);
if (resultNode2 != null) {
System.out.printf("找到了,信息為no=%d,name=%s\n", resultNode2.getNo(), resultNode2.getName());
System.out.println("遍歷次數:" + HeroNode.postCount);
} else {
System.out.println("沒有找到");
}
System.out.println("刪除3號節點");
binaryTree.delNo(3);
System.out.println("刪除后的節點");
binaryTree.preOrder();
/**
* 前序遍歷
* HeroNode{no=1, name=宋江}
* HeroNode{no=2, name=吳用}
* HeroNode{no=3, name=盧俊義}
* HeroNode{no=5, name=關勝}
* HeroNode{no=4, name=林沖}
* 中序遍歷
* HeroNode{no=2, name=吳用}
* HeroNode{no=1, name=宋江}
* HeroNode{no=5, name=關勝}
* HeroNode{no=3, name=盧俊義}
* HeroNode{no=4, name=林沖}
* 后續遍歷
* HeroNode{no=2, name=吳用}
* HeroNode{no=5, name=關勝}
* HeroNode{no=4, name=林沖}
* HeroNode{no=3, name=盧俊義}
* HeroNode{no=1, name=宋江}
* 前序遍歷查找~~
* 找到了,信息為no=5,name=關勝
* 遍歷次數:4
* 中序遍歷查找~~
* 找到了,信息為no=5,name=關勝
* 遍歷次數:3
* 后序遍歷查找~~
* 找到了,信息為no=5,name=關勝
* 遍歷次數:2
* 刪除3號節點
* 刪除后的節點
* HeroNode{no=1, name=宋江}
* HeroNode{no=2, name=吳用}
*/
}
}
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//前序遍歷
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
}
}
//中序遍歷
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
}
}
//刪除節點
public void delNo(int no) {
if (this.root != null) {
if (this.root.getNo() == no) {
this.root = null;
} else {
this.root.delNo(no);
}
}
return;
}
//后序遍歷
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
}
}
//前序遍歷查找
public HeroNode preOrderSearch(int no) {
if (root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//中序遍歷查找
public HeroNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
} else {
return null;
}
}
//后序遍歷查找
public HeroNode postOrderSearch(int no) {
if (root != null) {
return root.postOrderSearch(no);
} else {
return null;
}
}
}
class HeroNode {
static int preCount = 0;
static int infoxCount = 0;
static int postCount = 0;
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name=" + name +
'}';
}
//前序遍歷
public void preOrder() {
System.out.println(this);
//遞歸向左子樹前序遍歷
if (this.left != null) {
this.left.preOrder();
}
//遞歸向右子樹前序遍歷
if (this.right != null) {
this.right.preOrder();
}
}
//中序遍歷
public void infixOrder() {
//遞歸向左子樹中序遍歷
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
//遞歸向右子樹中序遍歷
if (this.right != null) {
this.right.infixOrder();
}
}
//后序遍歷
public void postOrder() {
//遞歸向左子樹后序遍歷
if (this.left != null) {
this.left.postOrder();
}
//遞歸向右子樹后序遍歷
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
//遞歸刪除節點
//1.如果刪除的節點是葉子節點,則刪除該節點。
//2.如果刪除的節點是非葉子節點,則刪除該樹。
public void delNo(int no) {
/**
* 1.因為我們的二叉樹是單向的,所以我們是判斷當前節點的子節點是否是需要刪除的節點,而不能去判斷當前節點是否是需要刪除的節點。
* 2.如果當前節點的左子節點不為空,并且左子節點就是需要刪除的節點,就將this.left = null;并且返回(結束遞歸)。
* 3.如果當前節點的右子節點不為空,并且右子節點就是需要刪除的節點,將將this.right = null;并且返回(結束遞歸)。
* 4.如果第2步和第3步沒有刪除節點,那么就要向左子樹進行遞歸刪除。
* 5.如果第4步也沒有刪除節點,則應當向右子樹進行遞歸刪除。
*/
if (this.left != null && this.left.no == no) {
this.left = null;
return;
}
if (this.right != null && this.right.no == no) {
this.right = null;
return;
}
if (this.left != null) {
this.left.delNo(no);
}
if (this.right != null) {
this.right.delNo(no);
}
}
//前序遍歷查找
public HeroNode preOrderSearch(int no) {
HeroNode res = null;
preCount++;//這里必須放在this.no == no 判斷之前,才進行實際的比較
//若果找到,就返回
if (this.no == no) {
return this;
}
//沒有找到,向左子樹遞歸進行前序查找
if (this.left != null) {
res = this.left.preOrderSearch(no);
}
//如果res != null 就直接返回
if (res != null) {
return res;
}
//如果左子樹沒有找打,向右子樹進行前序查找
if (this.right != null) {
res = this.right.preOrderSearch(no);
}
//如果找到就返回
if (res != null) {
return res;
}
return res;
}
//中序遍歷查找
public HeroNode infixOrderSearch(int no) {
HeroNode res = null;
if (this.left != null) {
res = this.left.infixOrderSearch(no);
}
if (res != null) {
return res;
}
infoxCount++;//這里必須放在this.no == no 判斷之前,才進行實際的比較
if (this.no == no) {
return this;
}
if (this.right != null) {
res = this.right.infixOrderSearch(no);
}
if (res != null) {
return res;
}
return res;
}
//后序遍歷查找
public HeroNode postOrderSearch(int no) {
HeroNode res = null;
if (this.left != null) {
res = this.left.postOrderSearch(no);
}
if (res != null) {
return res;
}
if (this.right != null) {
res = this.right.postOrderSearch(no);
}
if (res != null) {
return res;
}
postCount++;//這里必須放在this.no == no 判斷之前,才進行實際的比較
if (this.no == no) {
return this;
}
return res;
}
}
原文地址:https://www.toutiao.com/i6935051711136416287/