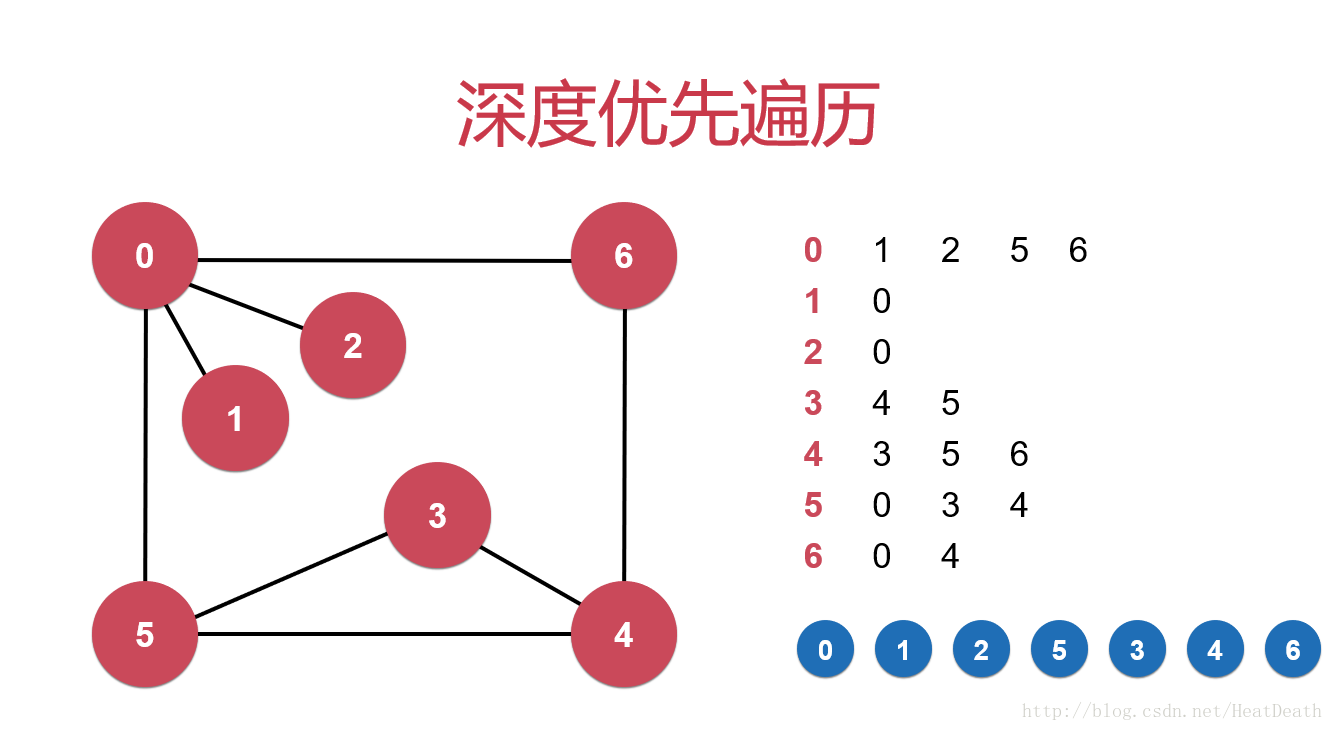
深度優(yōu)先遍歷類似于一個人走迷宮:

如圖所示,從起點開始選擇一條邊走到下一個頂點,沒到一個頂點便標記此頂點已到達。
當來到一個標記過的頂點時回退到上一個頂點,再選擇一條沒有到達過的頂點。
當回退到的路口已沒有可走的通道時繼續(xù)回退。
而連通分量,看概念:無向圖g的極大連通子圖稱為g的連通分量( connected component)。任何連通圖的連通分量只有一個,即是其自身,非連通的無向圖有多個連通分量。
下面看看具體實例:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
|
package com.datastructure.graph;// 求無權圖的聯(lián)通分量public class components { private graph graph; // 存放輸入的數(shù)組 private boolean[] visited; // 存放節(jié)點被訪問狀態(tài) private int componentcount; // 連通分量的數(shù)量 private int[] mark; // 存儲節(jié)點所屬聯(lián)通分量的標記 // 構造函數(shù),初始化私有屬性 public components(graph graph) { this.graph = graph; componentcount = 0; // 連通分量初始數(shù)量為 0 visited = new boolean[graph.v()]; mark = new int[graph.v()]; for (int i = 0; i < graph.v(); i++) { visited[i] = false; // 節(jié)點初始訪問狀態(tài)為 false mark[i] = -1; // 節(jié)點初始連通分量標記為 -1 } for (int i = 0; i < graph.v(); i++) { // 對于未被訪問的節(jié)點進行 dfs深度優(yōu)先遍歷 if (!visited[i]) { dfs(i); componentcount++; // 對一個節(jié)點進行dfs 到底后,一個連通分量結束,數(shù)量+1 } } } private void dfs(int i) { visited[i] = true; // 節(jié)點 i 已被訪問 mark[i] = componentcount; // 節(jié)點 i 屬于當前連通分量的數(shù)量(標記) for (int node : graph.adjacentnode(i)) { // 遍歷圖中節(jié)點 i 的鄰接節(jié)點 if (!visited[node]) // 對未被訪問的鄰接節(jié)點進行 dfs dfs(node); } } public boolean isconnected(int v, int w) { return mark[v] == mark[w]; // 根據(jù)兩節(jié)點所屬連通分量的標記判斷兩節(jié)點是否相連 } public int getcomponentcount() { return componentcount; // 返回 graph 中連通分量的數(shù)量 }}//public class components {//// private graph g; // 圖的引用// private boolean[] visited; // 記錄dfs的過程中節(jié)點是否被訪問// private int ccount; // 記錄聯(lián)通分量個數(shù)// private int[] id; // 每個節(jié)點所對應的聯(lián)通分量標記//// // 圖的深度優(yōu)先遍歷// private void dfs(int v) {//// visited[v] = true; // 節(jié)點 v 的訪問狀態(tài)置為 true// id[v] = ccount; // 節(jié)點 v 對應的聯(lián)通標記設置為 ccount//// // 遍歷節(jié)點 v 的鄰接點 i// for (int i : g.adjacentnode(v)) {// // 如果鄰接點 i 尚未被訪問// if (!visited[i])// // 對鄰接點 i 進行深度優(yōu)先遍歷// dfs(i);// }// }//// // 構造函數(shù), 求出無權圖的聯(lián)通分量// public components(graph graph) {//// // 算法初始化// g = graph;//// // visited 數(shù)組存儲 圖g 中 節(jié)點的被訪問狀態(tài)// visited = new boolean[g.v()];//// // id 數(shù)組存儲 圖g 中 節(jié)點所屬連通分量的標記// id = new int[g.v()];//// // 連通分量數(shù)量初始化為 0// ccount = 0;//// // 將 visited 數(shù)組全部置為 false; id 數(shù)組全部置為 -1// for (int i = 0; i < g.v(); i++) {// visited[i] = false;// id[i] = -1;// }//// // 求圖的聯(lián)通分量// for (int i = 0; i < g.v(); i++)// // 訪問一個未曾被訪問的節(jié)點// if (!visited[i]) {// // 對其進行深度優(yōu)先遍歷// dfs(i);// ccount++;// }// }//// // 返回圖的聯(lián)通分量個數(shù)// int count() {// return ccount;// }//// // 查詢點v和點w是否聯(lián)通(節(jié)點v 和 w 的聯(lián)通分量的標記是否相同// boolean isconnected(int v, int w) {// assert v >= 0 && v < g.v();// assert w >= 0 && w < g.v();// return id[v] == id[w];// }//} |
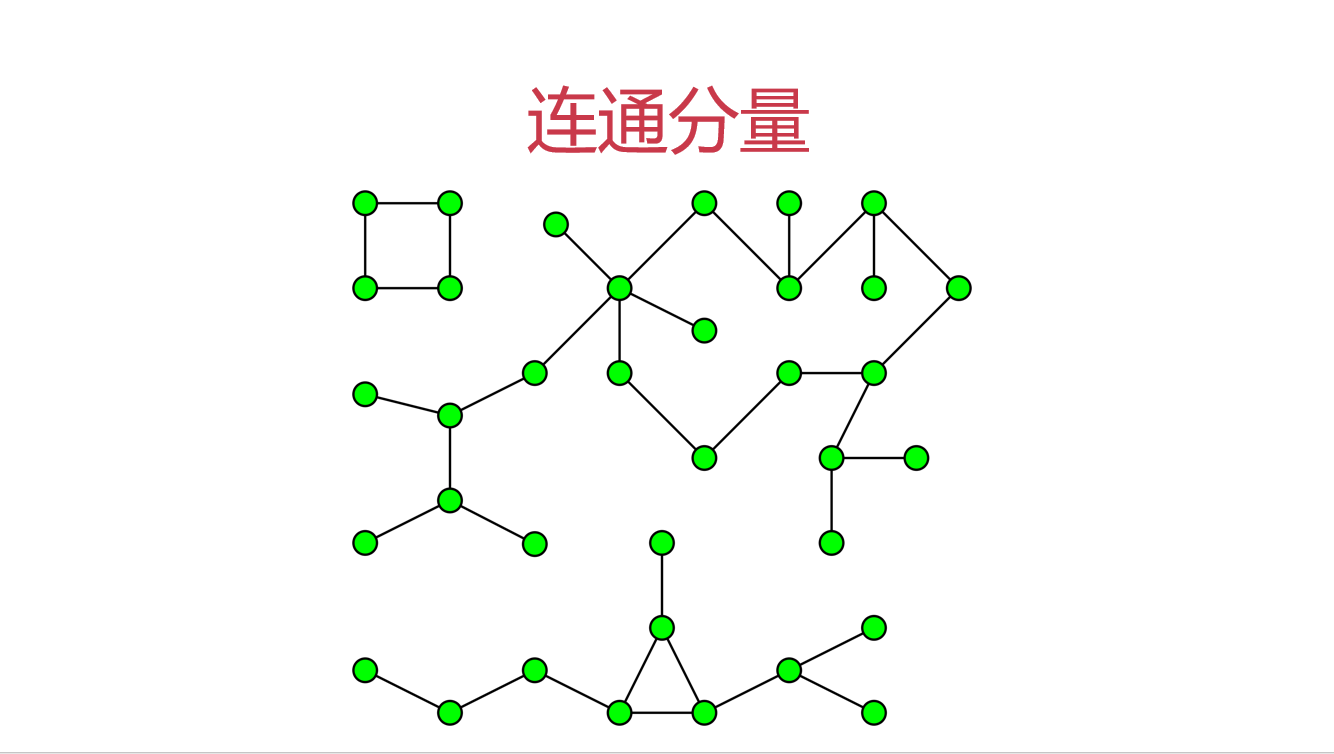
通分量數(shù)量為 3
總結
以上就是本文關于java編程實現(xiàn)深度優(yōu)先遍歷與連通分量代碼示例的全部內容,希望對大家有所幫助。如有不足之處,歡迎留言指出。關注服務器之家,您會有更多收獲。
原文鏈接:http://blog.csdn.net/heatdeath/article/details/78587762