国产成人在线播放,奇米久久,日韩一区二区三区视频

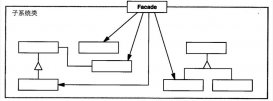
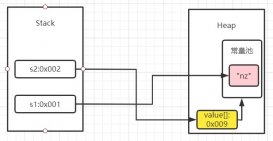
本文實例講述了java分治法與二分搜索算法。分享給大家供大家參考，具體如下：

1、分治法

分治法的基本思想是將一個規模為n的問題分解為k個規模較小的子問題，這些子問題相互獨立且與原問題相同。遞歸的解這些子問題，然后將各子問題的解合并得到原問題的解。

分治法所能解決的問題一般具有以下幾個特征：

　 1) 該問題的規模縮小到一定的程度就可以容易地解決
　 2) 該問題可以分解為若干個規模較小的相同問題，即該問題具有最優子結構性質。
　 3) 利用該問題分解出的子問題的解可以合并為該問題的解；
　 4) 該問題所分解出的各個子問題是相互獨立的，即子問題之間不包含公共的子子問題。

分治法的基本步驟：

分治法在每一層遞歸上都有三個步驟：

　　分解：將原問題分解為若干個規模較小，相互獨立，與原問題形式相同的子問題；
　　解決：若子問題規模較小而容易被解決則直接解，否則遞歸地解各個子問題；
　　合并：將各個子問題的解合并為原問題的解。

它的一般的算法設計模式如下：

									divide-and-conquer(p)

									if |p|≤n0

									then return(adhoc(p))

									//將p分解為較小的子問題 p1 ,p2 ,...,pk

									for i←1 to k

									do yi ← divide-and-conquer(pi) △ 遞歸解決pi

									t ← merge(y1,y2,...,yk) △ 合并子問題

									return(t)

其中|p|表示問題p的規模；n0為一閾值，表示當問題p的規模不超過n0時，問題已容易直接解出，不必再繼續分解。adhoc(p)是該分治法中的基本子算法，用于直接解小規模的問題p。因此，當p的規模不超過n0時直接用算法adhoc(p)求解。算法merge(y1,y2,...,yk)是該分治法中的合并子算法，用于將p的子問題p1,p2 ,...,pk的相應的解y1,y2,...,yk合并為p的解。

子問題的劃分：人們從大量實踐中發現，在用分治法設計算法時，最好使子問題的規模大致相同。換句話說，將一個問題分成大小相等的k個子問題的處理方法是行之有效的。許多問題可以取 k = 2。這種使子問題規模大致相等的做法是出自一種平衡(balancing)子問題的思想，它幾乎總是比子問題規模不等的做法要好。

2、二分搜索

大部分程序員應該都知道二分搜索的大致原理，這里不再贅述。需要說明的是二分搜索是所有以比較為基礎的搜索算法時間復雜度最低的算法。用二叉樹描速二分查找算法，最壞情況下與二叉樹的最高階相同。比較二叉樹線性查找也可用二叉樹表示，最壞情況下比較次數為數組元素數量。任何一種以比較為基礎的搜索算法，其最壞情況所用時間不可能低于o(logn)。

Java分治法與二分搜索算法實例分析

二分搜索程序清單如下：

									import java.util.scanner;

									public class binarysearch {

									  public static int binarysearch (int[] a,int x,int n) {

									    int left = 0;

									    int right = n - 1;

									    while(left <= right) {

									      int middle = (left + right) / 2;

									      if(x == a[middle]) return middle;

									      if(x >= a[middle]) left = middle + 1;

									      else right = middle - 1;

									    }

									    return -1;

									  }

									  public static void main(string args[]) {

									    system.out.println("服務器之家測試結果：");

									    int[] a = new int[10];

									    for(int i = 0; i < a.length; i++) {

									      a[i] = i+1;

									      system.out.print(a[i] + " ");

									    }

									    system.out.println();

									    system.out.println("請輸入你要查詢的數：");

									    scanner sc = new scanner(system.in);

									    int b = sc.nextint();

									    int num = binarysearch(a, b, a.length) + 1;

									    system.out.println("要查找的數在第" + num + "個位置");

									  }

									}