真正的幫助大家理解紅黑樹:
一、紅黑樹所處數據結構的位置:
在jdk源碼中, 有treemap和jdk8的hashmap都用到了紅黑樹去存儲
紅黑樹可以看成b樹的一種:
從二叉樹看,紅黑樹是一顆相對平衡的二叉樹
二叉樹-->搜索二叉樹-->平衡搜索二叉樹--> 紅黑樹
從n階樹看,紅黑樹就是一顆 2-3-4樹
n階樹-->b(b-)樹
故我提取出了紅黑樹部分的源碼,去說明紅黑樹的理解
看之前,理解紅黑樹的幾個特性,后面的操作都是為了讓樹符合紅黑樹的這幾個特性,從而滿足對查找效率的o(logn)
二、紅黑樹特性,以及保持的手段
1.根和葉子節(jié)點都是黑色的
2.不能有有連續(xù)兩個紅色的節(jié)點
3.從任一節(jié)點到它所能到達得葉子節(jié)點的所有簡單路徑都包含相同數目的黑色節(jié)點
這幾個特效,個人理解就是規(guī)定了紅黑樹是一顆2-3-4的b樹了,從而滿足了o(logn)查找效率
保持特性的手段,通過下面這些手段,讓紅黑樹滿足紅黑樹的特性,如果要嘗試理解,可以從2-3-4樹的向上增長,后面有詳細介紹
當然,這些改變也都是在o(logn)內完成的,主要改變方式有
1.改變顏色
2.左旋
3.右旋
三、從jdk源碼來理解
主要看我的注釋,邏輯的理解
先看treemap
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
|
//對treemap的紅黑樹理解注解. 2017.02.16 by 何錦彬 jdk,1.7.51<br> <br>/** from clr */ private void fixafterinsertion(entry<k, v> x) { //新加入紅黑樹的默認節(jié)點就是紅色 x.color = red; /** * 1. 如為根節(jié)點直接跳出 */ while (x != null && x != root && x.parent.color == red) { if (parentof(x) == leftof(parentof(parentof(x)))) { //如果x的父節(jié)點(p)是其父節(jié)點的父節(jié)點(g)的左節(jié)點 //即 下面這種情況 /** * g * p(red) u */ //獲取其叔(u)節(jié)點 entry<k, v> y = rightof(parentof(parentof(x))); if (colorof(y) == red) { // 這種情況,對應下面 圖:情況一 /** * g * p(red) u(red) * x */ //如果叔節(jié)點是紅色的(父節(jié)點有判斷是紅色). 即是雙紅色,比較好辦,通過改變顏色就行. 把p和u都設置成黑色然后,x加到p節(jié)點。 g節(jié)點當作新加入節(jié)點繼續(xù)迭代 setcolor(parentof(x), black); setcolor(y, black); setcolor(parentof(parentof(x)), red); x = parentof(parentof(x)); } else { //處理紅父,黑叔的情況 if (x == rightof(parentof(x))) { // 這種情況,對應下面 圖:情況二 /** * g * p(red) u(black) * x */ //如果x是右邊節(jié)點 x = parentof(x); // 進行左旋 rotateleft(x); } //左旋后,是這種情況了,對應下面 圖:情況三 /** * g * p(red) u(black) * x */ // 到這,x只能是左節(jié)點了,而且p是紅色,u是黑色的情況 //把p改成黑色,g改成紅色,以g為節(jié)點進行右旋 setcolor(parentof(x), black); setcolor(parentof(parentof(x)), red); rotateright(parentof(parentof(x))); } } else { //父節(jié)點在右邊的 /** * g * u p(red) */ //獲取u entry<k, v> y = leftof(parentof(parentof(x))); if (colorof(y) == red) { //紅父紅叔的情況 /** * g * u(red) p(red) */ setcolor(parentof(x), black); setcolor(y, black); setcolor(parentof(parentof(x)), red); //把g當作新插入的節(jié)點繼續(xù)進行迭代 x = parentof(parentof(x)); } else { //紅父黑叔,并且是右父的情況 /** * g * u(red) p(red) */ if (x == leftof(parentof(x))) { //如果插入的x是左節(jié)點 /** * g * u(black) p(red) * x */ x = parentof(x); //以p為節(jié)點進行右旋 rotateright(x); } //右旋后 /** * g * u(black) p(red) * x */ setcolor(parentof(x), black); setcolor(parentof(parentof(x)), red); //以g為節(jié)點進行左旋 rotateleft(parentof(parentof(x))); } } } //紅黑樹的根節(jié)點始終是黑色 root.color = black; } |
再看看hashmap的實現,在hashmap中,在jdk8后開始用紅黑樹代替鏈表,查找由o(n) 變成了 o(logn)
源碼分析如下:
|
1
2
3
4
5
6
7
8
|
for (int bincount = 0; ; ++bincount) { if ((e = p.next) == null) { p.next = newnode(hash, key, value, null); //jdk8 的hashmap,鏈表到了8就需要變成顆紅黑樹了 if (bincount >= treeify_threshold - 1) // -1 for 1st treeifybin(tab, hash); break; } |
紅黑樹的維護代碼部分如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
|
//hashmap的紅黑樹平衡 static <k,v> treenode<k,v> balanceinsertion(treenode<k,v> root, treenode<k,v> x) { x.red = true; //死循環(huán)加變量定義,總感覺java很少這樣寫代碼 哈 for (treenode<k,v> xp, xpp, xppl, xppr;;) { //xp x父節(jié)點, xpp x的祖父節(jié)點, xppl 祖父左節(jié)點 xxpr 祖父右節(jié)點 if ((xp = x.parent) == null) { x.red = false; return x; } // 如果父節(jié)點是黑色, 或者xp父節(jié)點是空,直接返回 else if (!xp.red || (xpp = xp.parent) == null) return root; // 下面的代碼就和上面的很treemap像了, if (xp == (xppl = xpp.left)) { // 第一種情況, 賦值xppl //父節(jié)點是左節(jié)點的情況,下面這種 /** * g * p(red) u */ if ((xppr = xpp.right) != null && xppr.red) { //如果紅叔的情況 // 這種情況,對應下面 圖:情況一 /** * g * p(red) u(red) * x */ //改變其顏色, xppr.red = false; xp.red = false; xpp.red = true; x = xpp; } else { // 黑叔的情況 // 這種情況 /** * g * p(red) u(black) */ if (x == xp.right) { //如果插入節(jié)點在右邊 這種 // 這種情況,對應下面 圖:情況二 /** * g * p(red) u(black) * x */ //需要進行左旋 root = rotateleft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } //左旋后情況都是這種了,對應下面 圖:情況三 /** * g * p(red) u(black) * x */ // 到這,x只能是左節(jié)點了,而且p是紅色,u是黑色的情況 if (xp != null) { //把p改成黑色,g改成紅色, 以g為節(jié)點進行右旋 xp.red = false; if (xpp != null) { xpp.red = true; root = rotateright(root, xpp); } } } } else { //父節(jié)點在右邊的 /** * g * u p(red) */ //獲取u if (xppl != null && xppl.red) { //紅父紅叔的情況 /** * g * u(red) p(red) */ xppl.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.left) { //如果插入的x是右節(jié)點 /** * g * u(black) p(red) * x */ root = rotateright(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } //右旋后 /** * g * u(black) p(red) * x */ if (xp != null) { //把p改成黑色,g改成紅色, xp.red = false; if (xpp != null) { xpp.red = true; //以g節(jié)點左旋 root = rotateleft(root, xpp); } } } } } |
情況圖如下
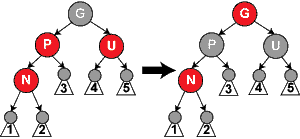
情況1
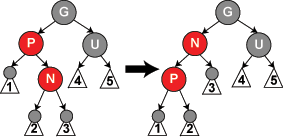
情況2
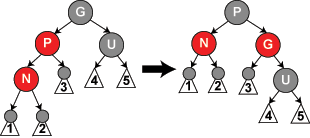
情況3
jdk源碼處理紅黑樹的流程圖
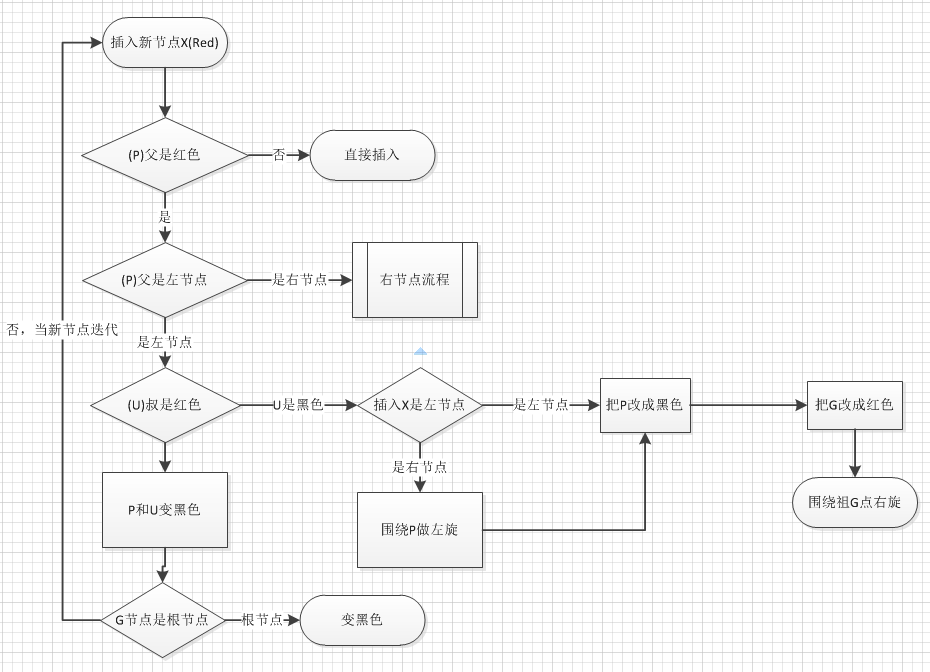
可見,其實處理邏輯實現都一樣的
三、個人對紅黑樹理解的方法
1. 如何理解紅黑樹的o(lgn)的特性?
從2-3-4樹去理解
紅黑樹,其實是一顆 2-3-4的b樹,b樹都是向上增長的,如果不理解向上增長可以先看看2-3樹,這樣理解就能知道為什么能o(logn)的查找了
2.如何理解紅黑樹的紅黑節(jié)點意義?
可以把紅色節(jié)點看成是連接父節(jié)點的組成的一個大節(jié)點(2個或3個或4個節(jié)點組成的一個key),如下:
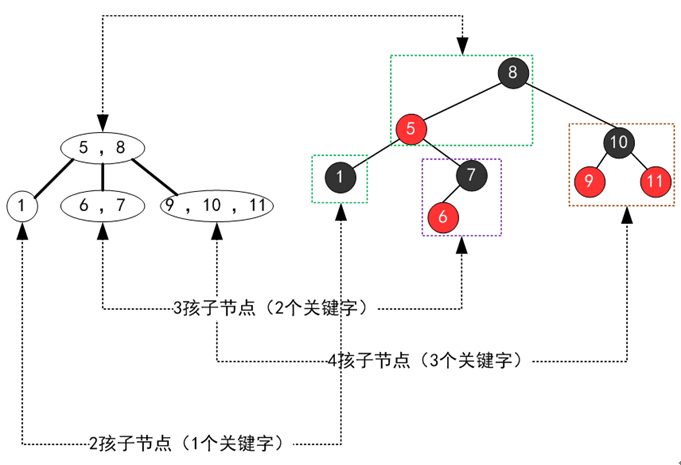
(此圖轉自網上)
紅色的就是和父節(jié)點組成了大節(jié)點,
比如
節(jié)點7和6,6是紅色節(jié)點組成,故和它父節(jié)點7組成了一個大節(jié)點,即 2-3-4樹的 6, 7節(jié)點
又如
節(jié)點 9和10和11,9和10為紅色節(jié)點,故和10組成了一個2-3-4的3階節(jié)點, 9,10,11(注意順序有的關性)
3.b樹是如何保持o(lgn)的復雜度的呢?
b+樹都是從底布開始往上生長,自動平衡,如 2-3-4樹,當節(jié)點達到了3個時晉升到上個節(jié)點,所以不會產生單獨生長一邊的情況,形成平衡。
留個問題
4.數據庫里的索引為什么不用紅黑樹而是用b+樹(mysql)呢?
后續(xù)解答
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持服務器之家。
原文鏈接:http://www.cnblogs.com/springsource/p/6419462.html